傾向スコアによるタクシーアプリ『GO』利用影響の分析

AI技術開発部分析グループの佐竹です。 分析グループは、タクシーアプリ「GO」におけるデータドリブンなビジネス意思決定を行うために、様々なユーザ分析、乗務員分析を行っています。 今回は統計的因果推論の手法のうち、傾向スコアを用いた因果効果の推定について紹介します。

はじめに

「GO」では、ユーザーや乗務員に対し実行している様々な施策があります。その中でも、ユーザー施策が今後の継続利用に与える影響を正しく把握し、次の施策に繋がるような示唆を見出していくことが分析として重要となる場合があります。

そこで、今回は上記の施策検証の際の分析について以下の流れで紹介します。

1. 施策を受けるか受けないか、がユーザーの利用状況によって異なることにより特徴に偏りが発生し、両者を単純比較できないという分析課題を確認
2. 1の課題を解決するため、統計的因果推論の手法である「傾向スコア」を用いて因果効果を推定する
3. ダミーデータに対し傾向スコアを適用した場合にデータの偏りが小さくなるのかを確認

分析における課題

まず、分析設計の例を挙げ、その中で課題となる箇所について説明します。

今回例として、初めて「GO」を利用した際に、施策を受けたユーザーとそうでないユーザーの離脱率を比較することを考えます。ただし注意点としては、「GO」利用時に需要と供給の状況がユーザー毎に異なることにより、施策を受けるか受けないか（施策の割り当て）、が異なる場合があります。需要と供給について、例えば、雨が降っている場合に需要が増加し、タクシーの供給量が不足してしまう、といったものです。そのため、施策を受けたグループ（処置群）とそうでないグループ（対照群）の特徴に偏りが出る可能性があり、その場合、両者を単純比較しても正しく効果量を推定できません。例えば、「いつ」「どこで」「どのような目的で」利用するか、といった利用シーンなどが偏りの原因となる可能性があります。

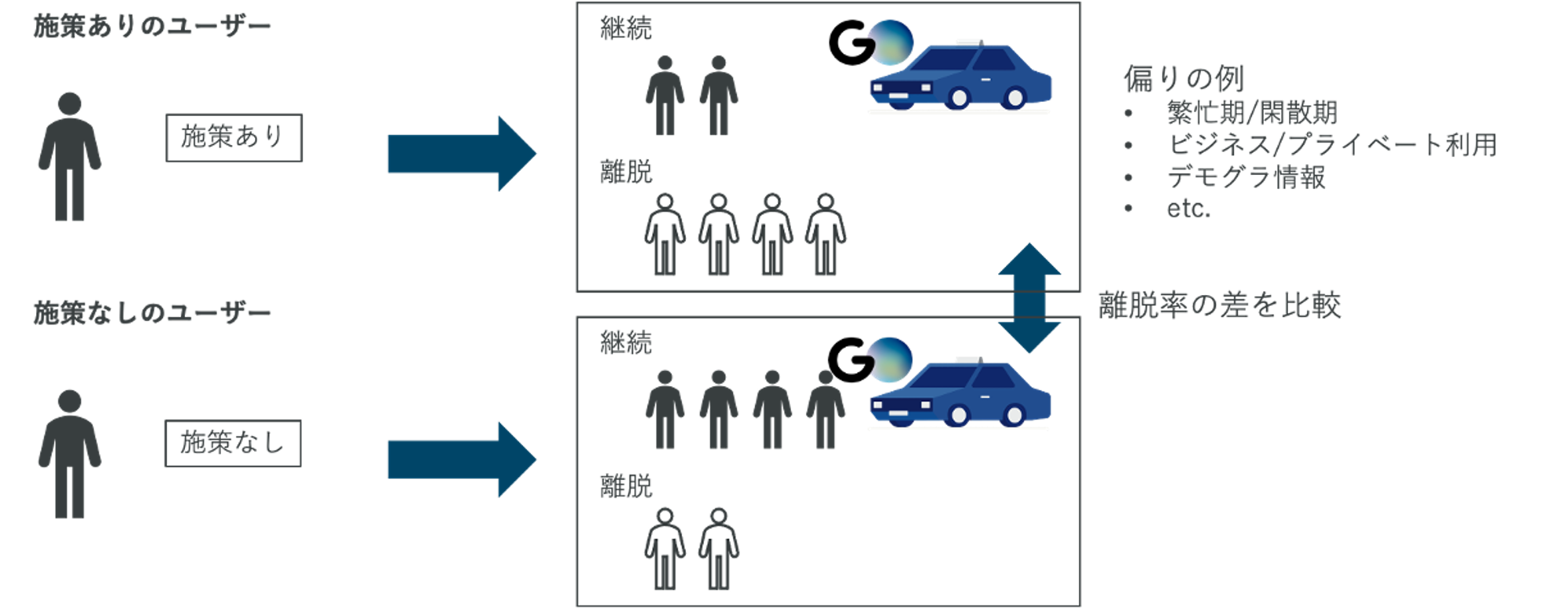
そこで、今回は処置群と対照群のデータに偏りがある、という課題に対し、統計的因果推論の手法によりデータの偏りを考慮した上で、離脱率の影響を推定します。

傾向スコアについて

統計的因果推論の前提となる考え方については、過去のブログや当社にて開催のイベントMoT TechTalk #9でも紹介していますので参照ください。 前述の通り、「GO」の利用シーンは様々で、例えば「いつ」「どこで」「どのような目的で」利用するか、など複数の特徴（以下、共変量）で構成されています。そのため、実務上何らかの施策を実施した際にも、施策が割り当てられたか、そうでないか、がランダムに選ばれず、結果に対してバイアスが発生します。それにより、処置群と対照群を単純比較できず、効果の解釈も困難となります。

そこで、処置群と対照群における処置の割り当て方の違いから生じるバイアスを調整し、よりフェアな比較を行う手法として「傾向スコア」を用いた因果効果の推定が挙げられます。

傾向スコアとは、対象者が共変量を前提条件として処置群に割り当てられる確率を表しています。

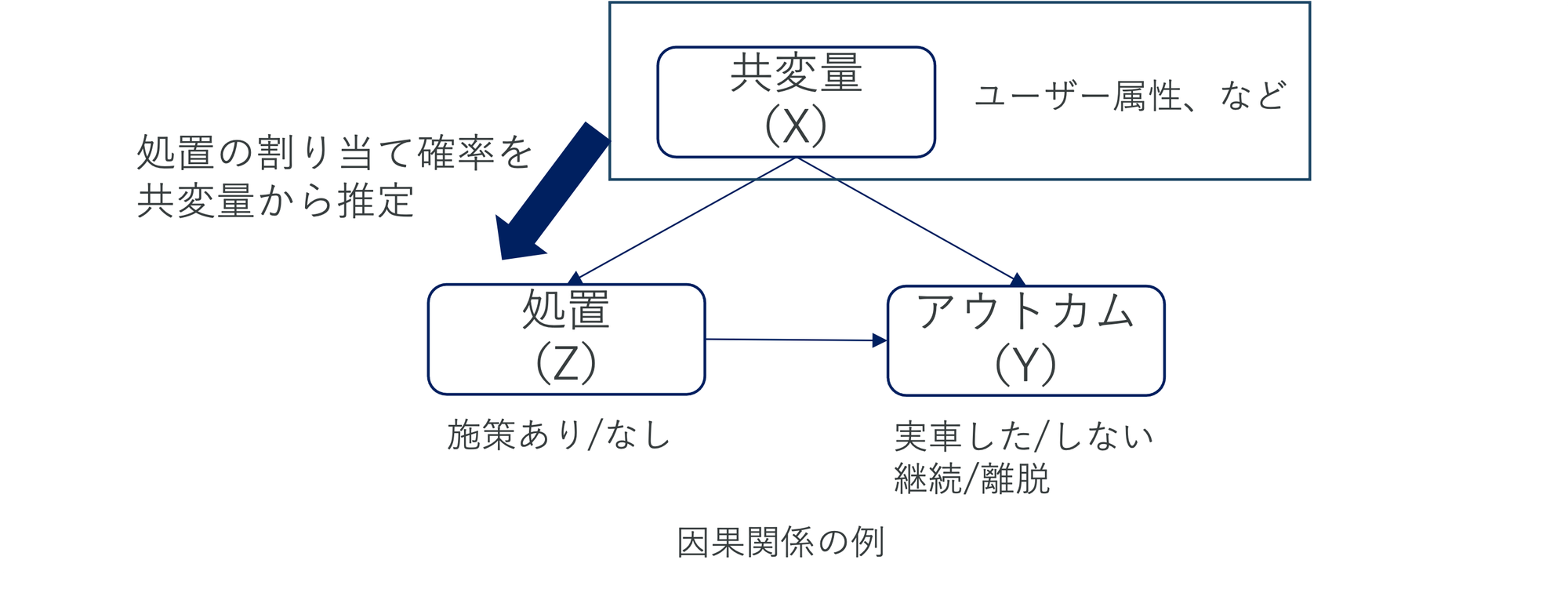
上図のような因果関係の場合、各ユーザー$i$の傾向スコア$e_i$を推定する際の共変量$X$と処置$Z$の関係は下式のように表されます。

傾向スコアは通常真値は観測できないため、何らかのモデルに基づき推定することになります。前述の通り、共変量$X$を説明変数、処置$Z$を目的変数としたモデルを構築しますが、ロジスティック回帰が用いられるケースが多く、その他ランダムフォレストや勾配ブースティングなど機械学習の手法を用いる場合もあります。

推定した傾向スコアを用いて、処置群と対照群のバイアスを調整した上で比較を行いますが、調整方法としては、処置群と対照群の傾向スコアが同一のペアを作成するマッチングや、傾向スコアの逆数の値を用いて重み付けを行うInverse Probability Weighting（IPW）などが挙げられます。

適用事例

それでは、適用事例について見ていきます。

事例としては、前述の通り、初めて「GO」を利用したユーザーに対する施策によって、離脱率がどの程度増加するか？について取り上げます。

利用データについて

今回は処置群（施策ありの群）と対照群（施策なしの群）のデータの質が同一となる（=共変量の分布が同一）ようにダミーデータを作成します。そして、ダミーデータから共変量の分布が偏るようにデータを抽出し実験を行います。

データには施策の有無、離脱の有無に加えて、「いつ（曜日や時間）」「どこで（地域）」利用したか、といった情報などが含まれています。

まず、実験に進む前に、ダミーデータにおける離脱率の差（真値）を見てみましょう。ここでは0.14となっています。

傾向スコアの推定

傾向スコアの推定について、変数は以下の通りとなります。

• アウトカム：今後Nヶ月後の離脱率
• 処置：初回利用時における施策の割り当ての有無
• 共変量：時間帯、曜日、場所、年齢、性別、など

処置と共変量を用いて、初回利用時に施策が割り当てられる確率をロジスティック回帰で推定し、IPWを用いて調整した後に両者の離脱率を比較します。

結果について

離脱率の差を見る前に、傾向スコアの適用前後でデータの偏りがどのように変化するのかを見ていきましょう。

以下のグラフでは、処置の割り当てに対し、共変量の分布が実験群と対照群で同じと言えるか、について、2つの共変量を例として挙げています。前述の通り、共変量の分布が偏っていると両群を単純比較することが難しくなります。以下のグラフについて、共変量の分布を表すヒストグラムのオレンジと青の分布がどの程度似ているかを見ていくと、傾向スコア適用前は分布が偏っている箇所が多いですが、適用後は分布の偏りが小さくなっています。

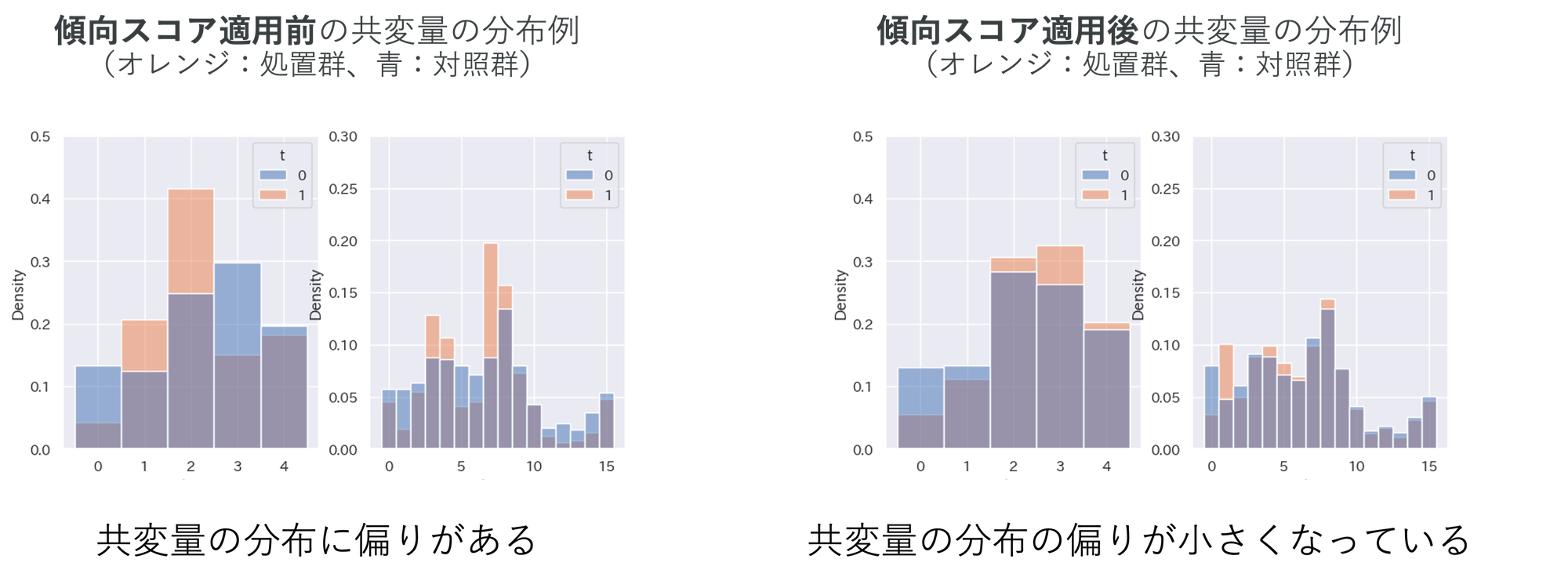
ただし、偏りが残っている箇所もあるため、ビジネス要件を満たした上で、ドメイン知識に基づいてデータを絞り込むなど、より偏りが小さくなるようなアプローチも分析の状況によっては考えていきます。

最後に効果量の推定について、傾向スコア適用後の離脱率が0.15とダミーデータの真値0.14に近づいていることが確認できます。

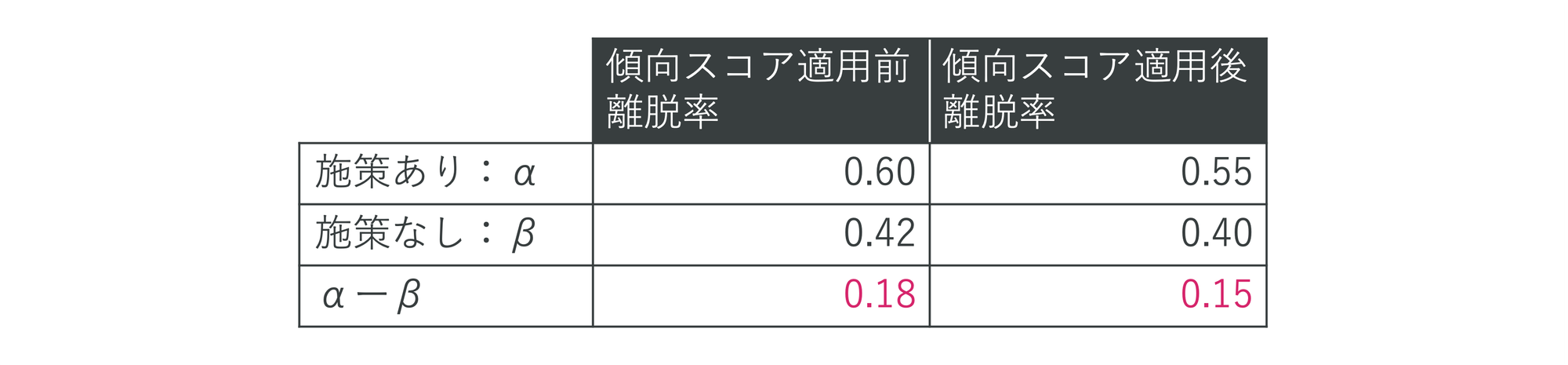
前述の通り、傾向スコアは真値が観測できないため、推定した効果量の妥当性の判断や解釈を行う際には、傾向スコア適用により処置群と対照群における共変量の分布の偏りが小さくなっているか、また、偏りがあった場合に何が考慮されていないのか、といった視点は必要になってきます。

最後に

今回は、統計的因果推論のうち、傾向スコアを用いて施策の効果量を推定する手法を紹介しました。

実務で活用する際には、統計的因果推論の各手法における前提条件を満たす必要があります。そして何よりも、「分析で明らかにしたいことは何か」「推定した効果量がビジネスとしてどのようなインパクトがあるのか」といった要件の考慮が重要であり、分析を行う場合に常に意識しながら取り組む必要があります。

We're Hiring!

興味のある方は 採用ページ も見ていただけると嬉しいです。

Twitter @mot_techtalk のフォローもよろしくお願いします！