入門 統計的因果推論

AI技術開発部分析グループマネージャーの島田です。分析グループは、タクシーアプリ「GO」におけるデータドリブンなビジネス意思決定を行うために、様々なユーザ分析、乗務員分析を行っています。本記事では、分析グループ内で開催した統計的因果推論の勉強会について紹介したいと思います。

勉強会のモチベーション

「データドリブンなビジネス意思決定」という文脈においては、機械学習モデルの精度を向上させる能力はあまり重要ではありません。どちらかといえば、物事をどうモデリングすべきか不明なケースで、状況を整理して課題を明確にし、適切に定式化したり、データ分析に落とし込む能力が重要で、その一助となるであろう「統計的因果推論」をチームのスキルとして身につけようということで勉強会を開始しました。つぎのような場面で統計的因果推論が活躍してくれることを期待しています。

A/Bテストでは効果なしとなったが、あるサブグループでは効果がありそうに見える。サブグループでのA/Bテスト再実験をせずに、手元のデータからサブグループ内での効果をアンバイアスに推定できないだろうか？

すでにリリースされてしまった新機能やUI変更が、ユーザのCVRに与える効果はどの程度と見積もれば良いだろうか？

"Introduction to Causal Inference"の紹介

「統計的因果推論」は長らく計量経済学や疫学の分野として発展してきましたが、ここ数年は機械学習の手法も合わさった発展を見せており、そこまで踏み込んで学習できるコンテンツはまだ多くはありません。また、社内勉強会ではコンテンツの準備に時間がかかってしまうと継続が難しくなってしまうので、自学自習できるレベルでコンテンツが揃っていてくれると助かります。そこで出会ったのが「Introduction to Causal Inference」という素晴らしいオンラインコースでした。

Yoshua Bengio先生が中心となってカナダのモントリオール大学で設立されたAI研究所であるMilaで開講されたコースで、講義資料やテキストブックが公開されているだけではなく、講義動画はYouTubeで公開され、Susan Athey先生、Alberto Abadie先生、Yoshua Bengio先生のゲストトークも閲覧可能ですし、参考文献も充実しています。

Course Schedule

私たちの勉強会では週1回開催で約4ヶ月ほどかけて統計的因果推論の理解を深めました。英語のみのコンテンツですが、動画もあるため理解は進めやすいと思います。ここでは各週でどのようなトピックについて学習するのか簡単に紹介したいと思います。

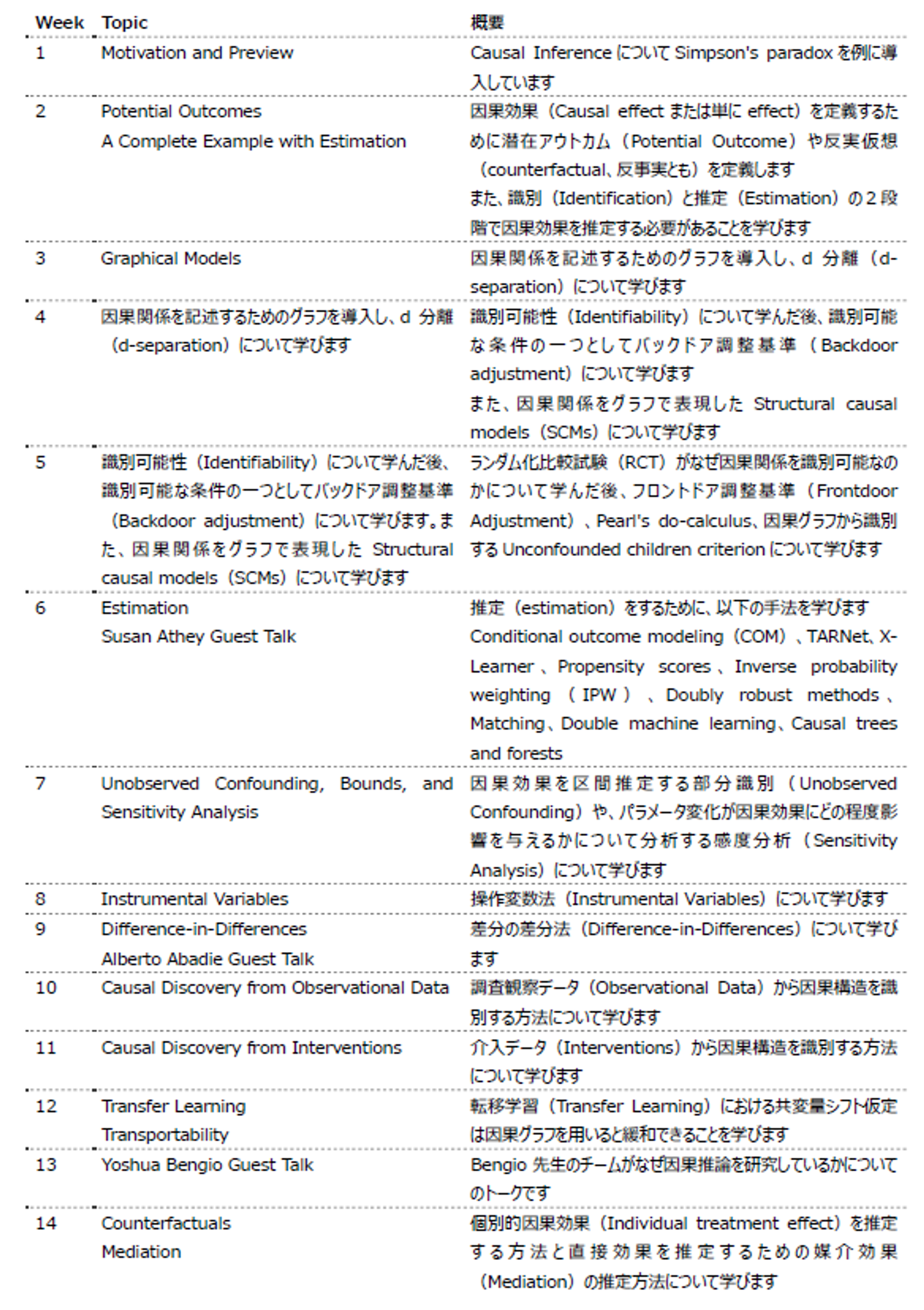
統計的因果推論とは

統計的因果推論がどのような問題設定に取り組もうとしているか雰囲気をつかんでいただければと思います。なお、Introduction to Causal Inferenceの1週目とほぼ同等の内容となっていますので、より詳しく学びたいという方はぜひコースを進めていただきたいです。

シンプソンのパラドックス

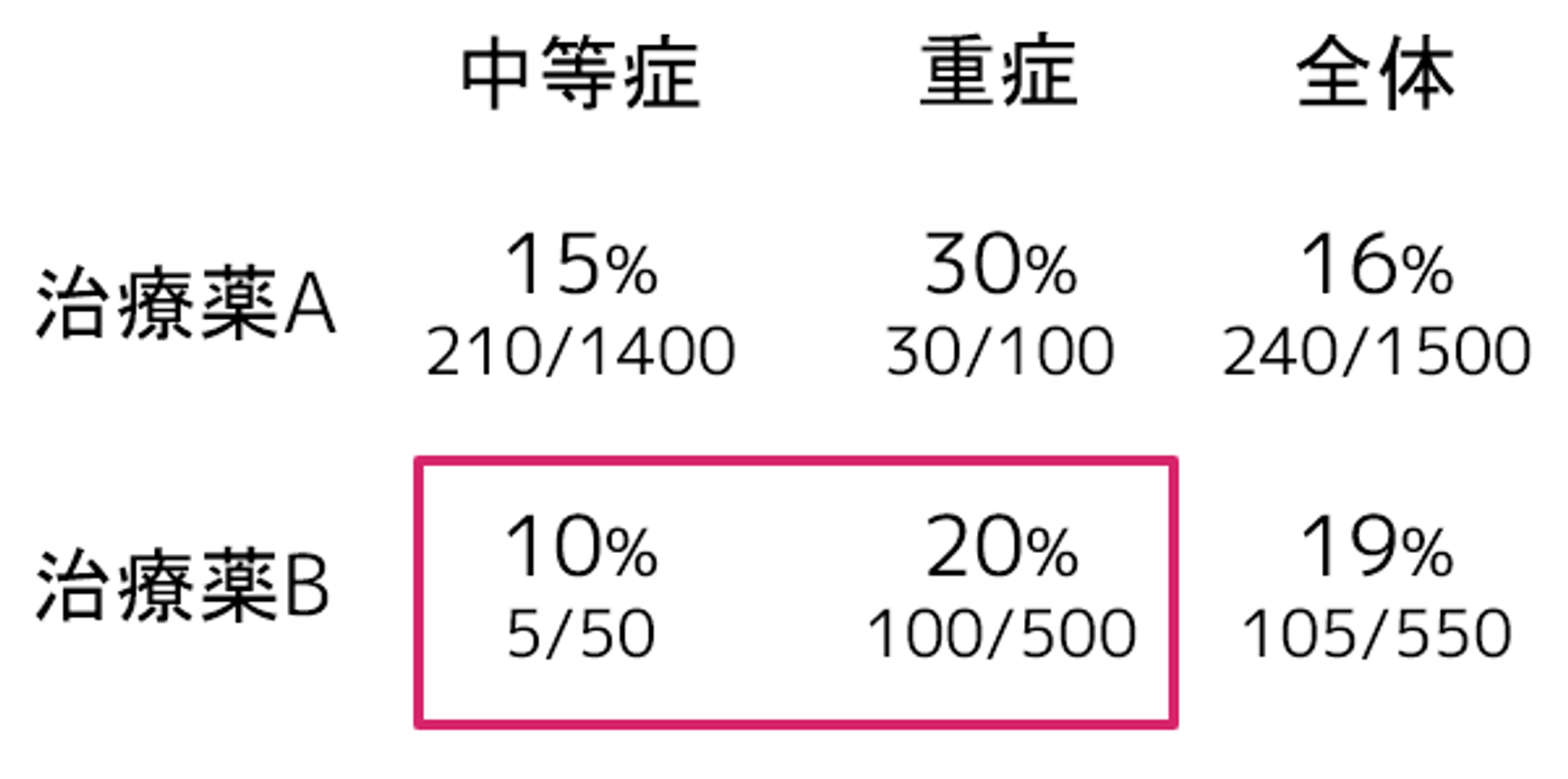
ある病気の治療薬Aと治療薬Bについて、中等症と重症のそれぞれの投与後の致命率を観察しました。症状別では治療薬Bが効果がありそうですが、全体では治療薬Aが効果がありそうな結果となっています。どちらの治療薬を今後採用すれば良いのでしょうか？

シナリオ1：症状が治療薬選択に影響を与えている

• 医者が症状に応じてどちらの治療薬を投与するか選択してます
• この場合は、症状別の効果を見る必要があります

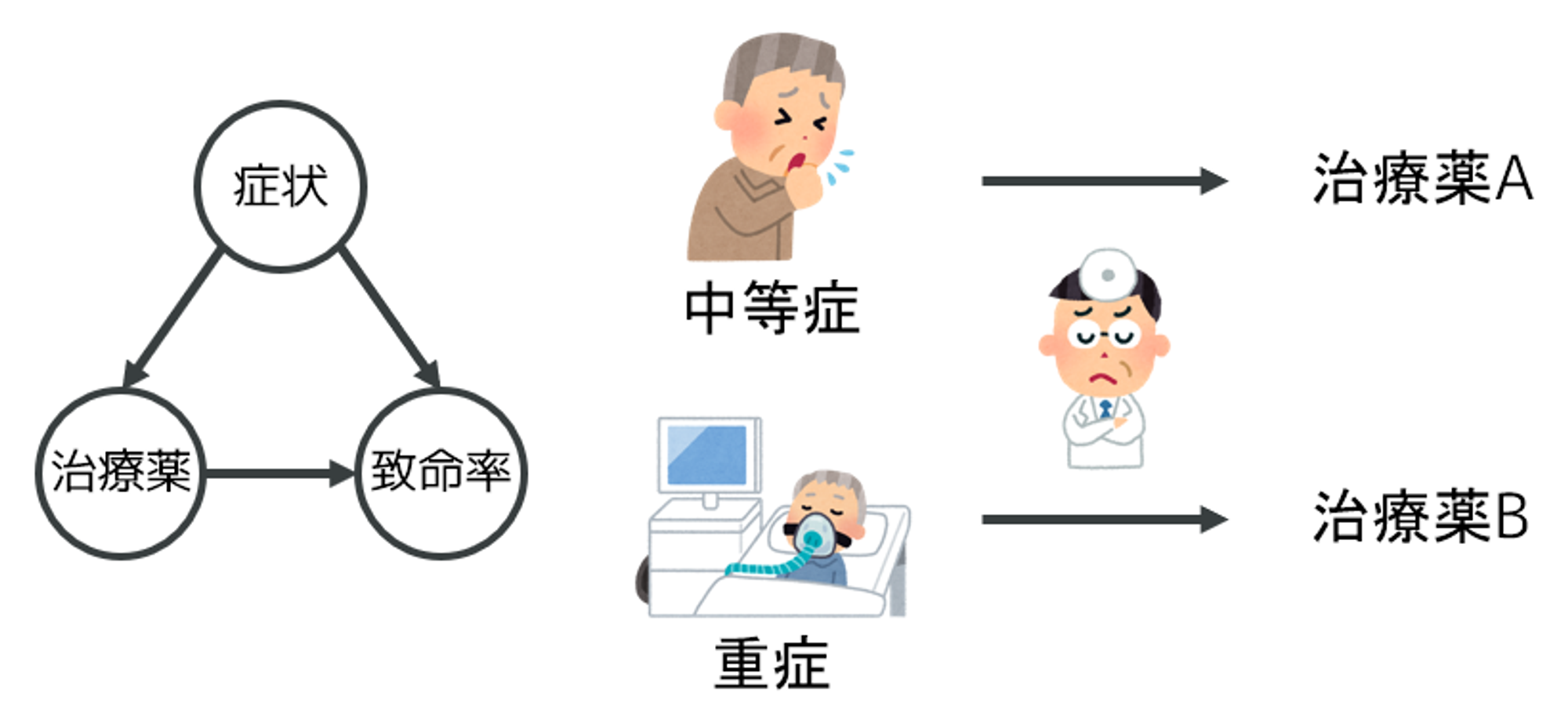
シナリオ2：治療薬が症状に影響を与えている

• 治療薬Aを選択すると、スムーズに治療を受けられて中等症で済むようです
• 治療薬Bを選択すると、治療開始まで時間がかかってしまい重症になってしまいます
• この場合は、全体の結果を見る必要があります

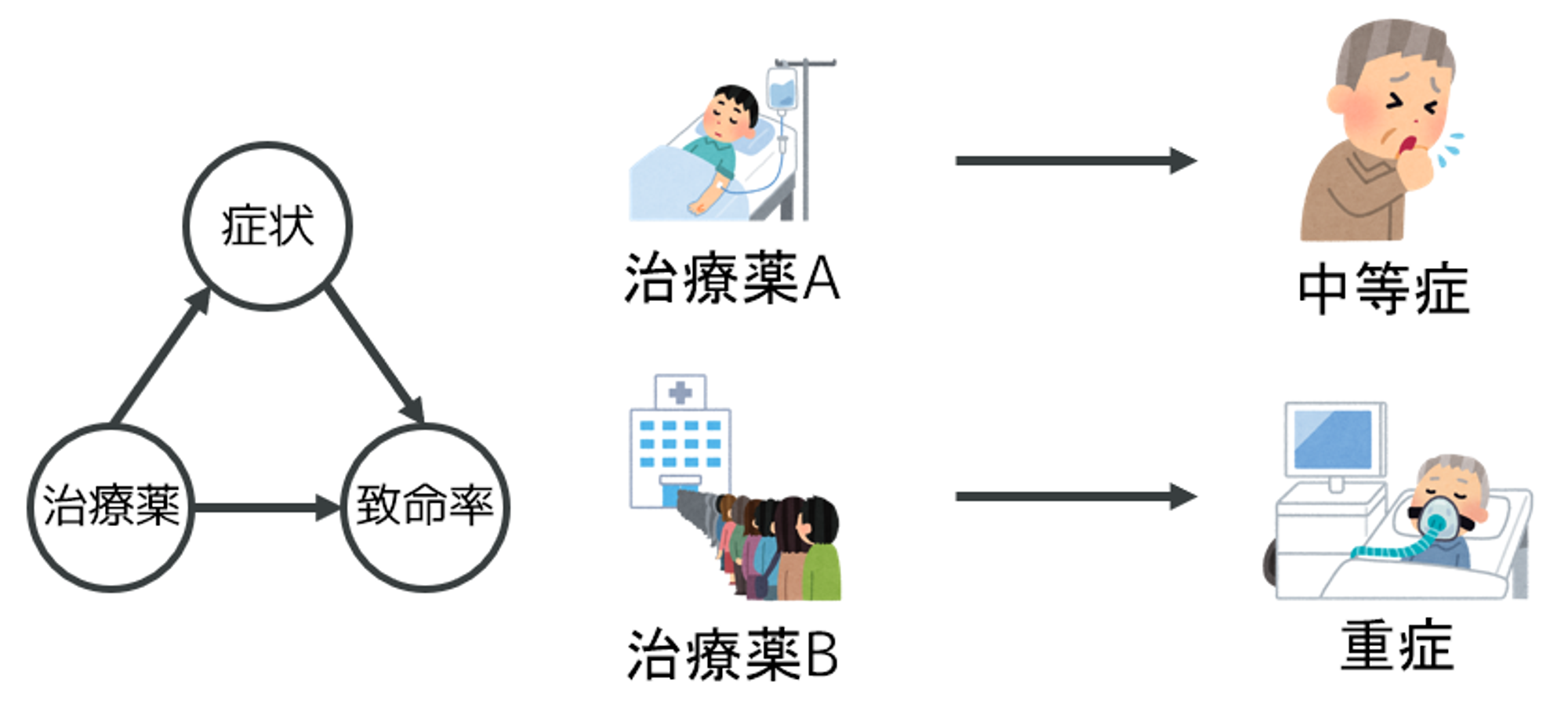
相関関係は因果関係を意味しない

「靴を履いたまま寝る」ことと「翌朝、頭痛がする」ことには非常に強い相関関係が表れました。これは、「靴を履いたまま寝る」ことと「翌朝、頭痛がする」ことに因果関係があることを意味するのでしょうか？

「靴を履いたまま寝る」ことと「翌朝、頭痛がする」ことの共通の原因として前日の夜に「お酒を飲む」ことがあったとすると、「靴を脱いで寝る」ことに大きな影響を与えていそうな交絡因子であることは想像に難くないです。相関関係がある場合に因果関係があると考えてしまうのは人間の思考の癖で、認知バイアスだということは認識しておきましょう。

因果関係とは？

薬を飲んで頭痛が治った場合と、薬を飲まなくて頭痛が治らなかった場合を観察できたとすると、薬が頭痛の回復に対する因果効果があると考えて良さそうです。

薬を飲んでも飲まなくても頭痛が治った場合はどうでしょうか？この場合は因果効果なしと考えることが正しそうです。

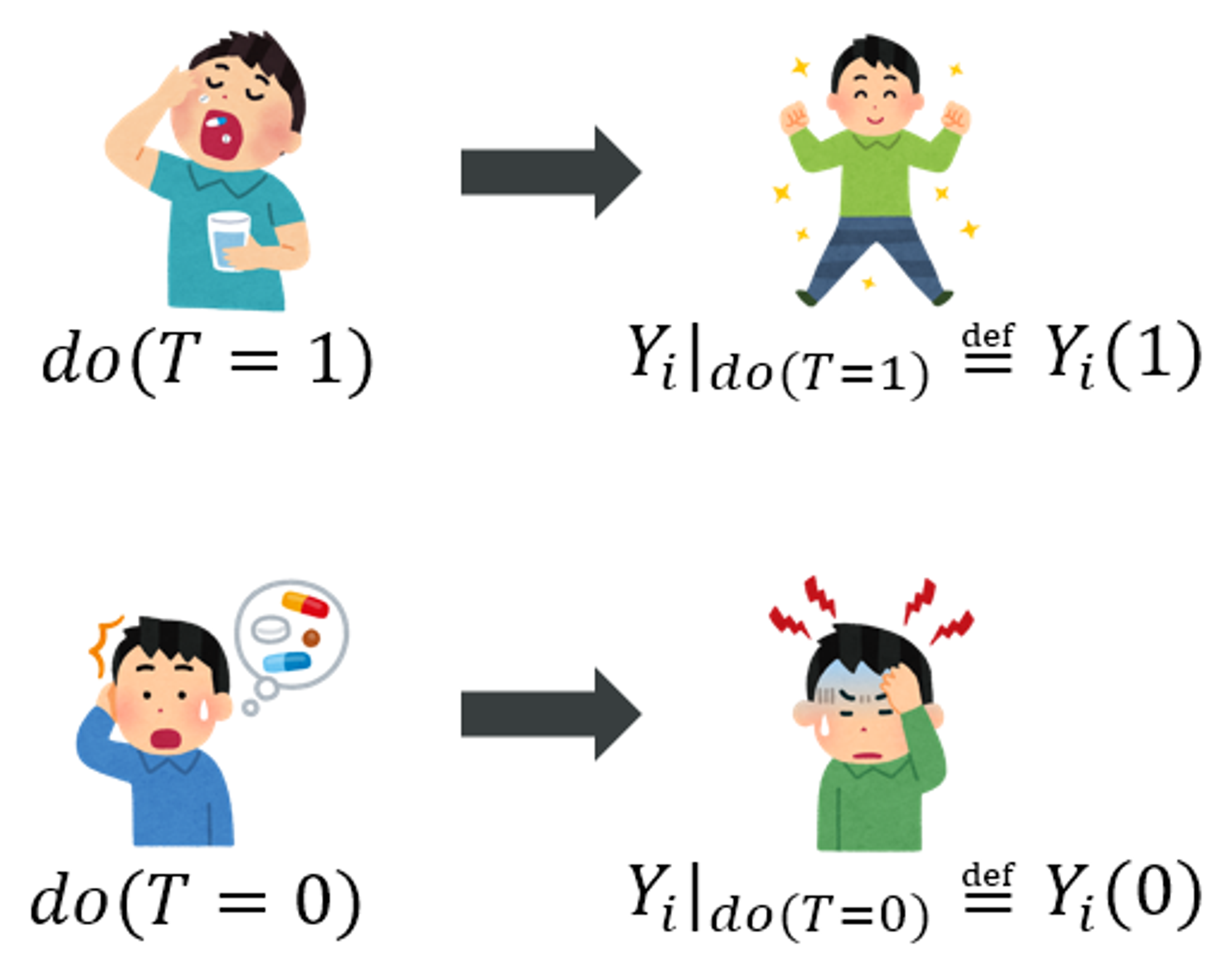
因果効果の定義

$T$を処置（Treatment）の有無として、$T=1$は薬を飲んだ場合、$T=0$は薬を飲まなかった場合を示すとします。$Y$を観察されたアウトカムとし、添え字の$i$は個人（unitあるいはindividual）とします。$Y_{i}(1)$は処置を受けた場合のポテンシャルアウトカムで、$Y_{i}(0)$は処置を受けなかった場合のポテンシャルアウトカムです。この定義の元で、因果効果（Causal effect）は$\bold{Y_{i}(1) - Y_{i}(0)}$と定義できます。

もう一歩理解を進めると、$Y_{i}(1) - Y_{i}(0)$は個別的因果効果（ITE: Individual Treatment Effect）と呼ばれるもので、一般に推定が難しいため、ある集団全体の平均因果効果（ATE: Average Treatment Effect）に着目することになります。平均因果効果の定義は$\mathbb{E}[Y_{i}(1)-Y_{i}(0)]=\mathbb{E}[Y_{i}(1)]-\mathbb{E}[Y_{i}(0)]$で、個別的因果効果の期待値を取っています。ただし、平均因果効果は条件付き期待値の差と一般には一致しません（$\mathbb{E}[Y_{i}(1)]-\mathbb{E}[Y_{i}(0)]\ne\mathbb{E}[Y|T=1]-\mathbb{E}[Y|T=0]$）。これは、靴を履いて寝た人が頭痛になる期待値と靴を履かずに寝た人が頭痛になる条件付き期待値の差が因果効果とはいえなかったことを思い出してもらえれば理解できると思います。

調査観察データにおける因果効果の推定方法

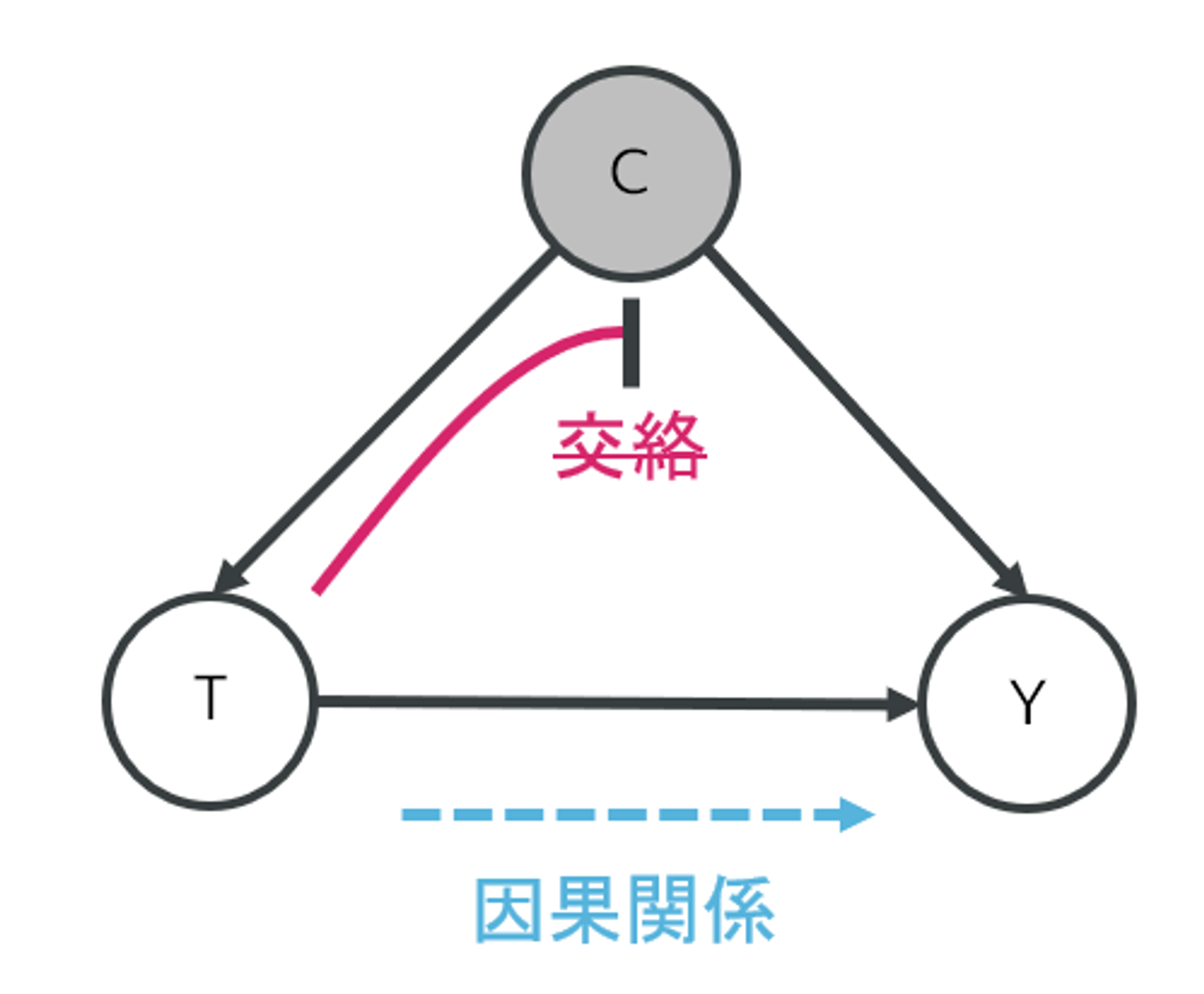
調査観察データにおいては、適切な調整因子$W$で調整することで処置とアウトカムの間の交絡のパスを閉じることができ、因果関係のパスのみを取り扱うことができます。$W$が十分な調整因子である（図中では交絡因子$C$（Confounders）が調整因子の条件を満たす）とすると、調整はつぎのように定義でき、簡単な例では$W$に具体的な値を与えたときと同じような操作になります。

治療薬選択問題

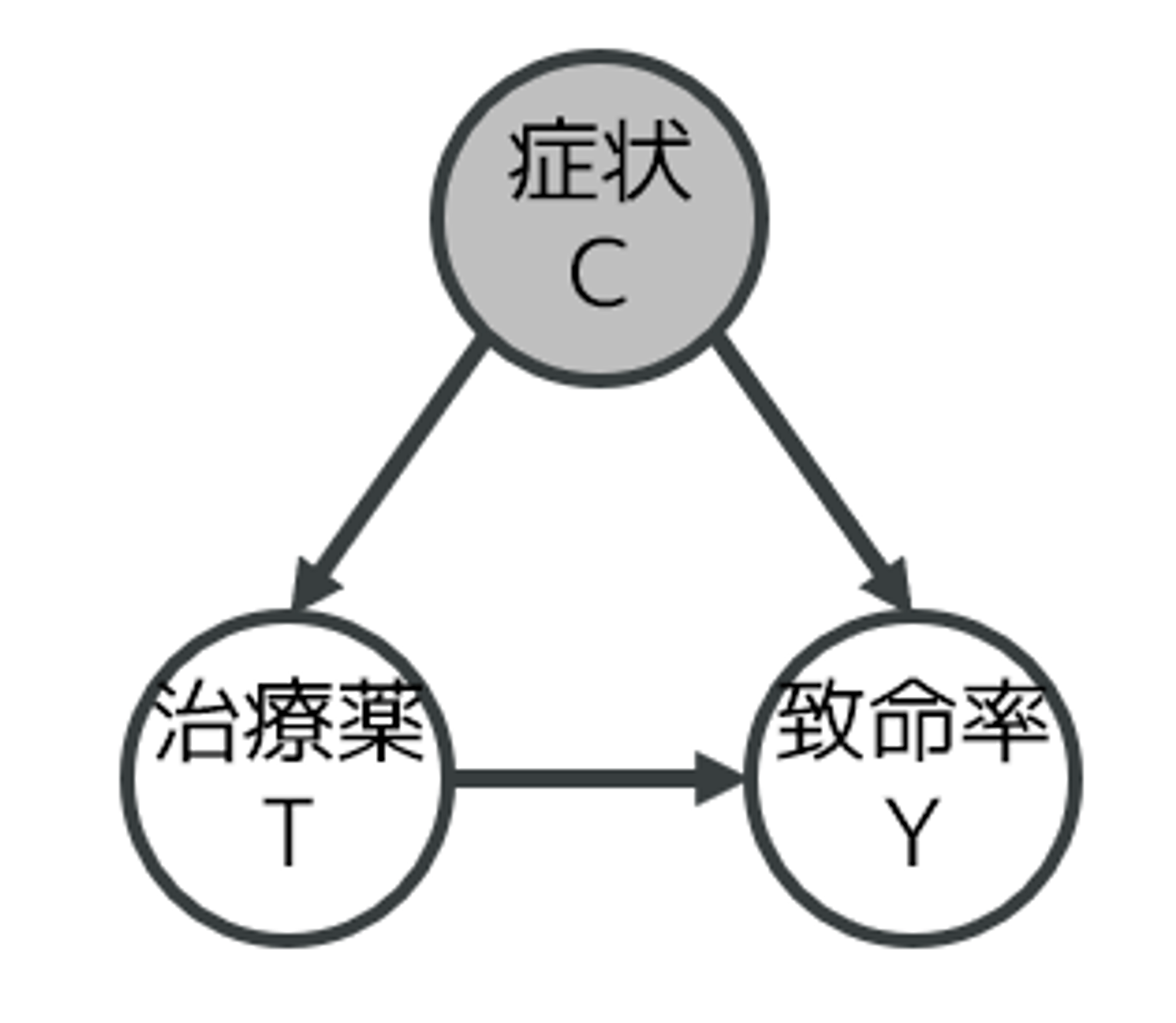
さて、シンプソンのパラドックスで紹介した治療薬選択問題に戻ってみましょう。症状が治療薬選択と致命率の両方に影響を与える交絡パスである場合、症状$C$で調整すれば因果効果が推定できるのでした。

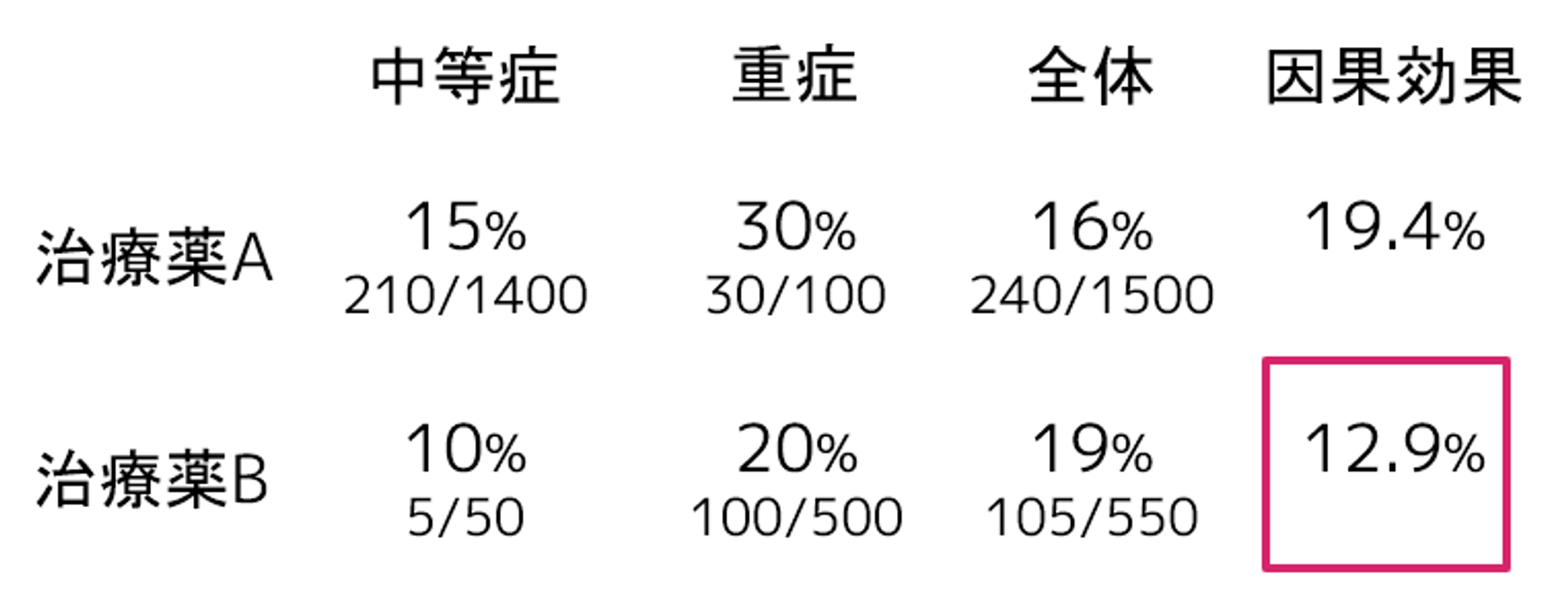
中等症の確率と重症の確率をかけることで調整できそうですので、以下のような計算で因果効果を推定できます。つまり、治療薬Bを選択することで致命率を下げることができそうということになります。

さいごに

シンプソンのパラドックスのように、データの取り扱いによって真逆の結論を導いてしまうことを考えると恐ろしいとともに、因果関係を明示的に取り扱うことで、このような問題に立ち向かえる可能性を感じられるのは非常に面白いですね。私たちAI技術開発部分析グループでは、仲間同士でスキルアップをしながらデータドリブンなビジネス意思決定を主導していきたいと考えています。

We're Hiring!