ETA(到着予想時間)の重要性と「通り過ぎ問題」への対策

AI技術開発部アルゴリズムグループの齋藤です。

今回は弊社が提供するタクシーアプリ「GO」における非常に大事な到着予想時間(Estimated Time of Arrival, ETA)とは何か、精度向上のためにどのような工夫をしているのかについて紹介させていただきます。

はじめに

本記事では、私の所属するアルゴリズムグループを含め多くの方が関わっているETAについて

• ETAとは何か
• 何が難しいのか
• 技術的にどのような工夫をしているのか

について詳しく紹介していきます。

ETAと言われると日頃馴染みのない概念なのかと思いますが、この記事を読むことでタクシーアプリ「GO」のみではなく、実は皆さんにとっても身近なものだということがわかるかと思います。

できるだけわかりやすく書いたつもりですので、是非気軽に読んでいただければと思います。

ETAとは

最初に「ETA」とは何かについて説明します。

ETAは Estimated Time of Arrival の略、日本語では 「到着予想時間」 のように訳しますが、具体的には、図に示すような「ある地点Aからある地点Bに行くまでの到着予測時間」のことを示します。

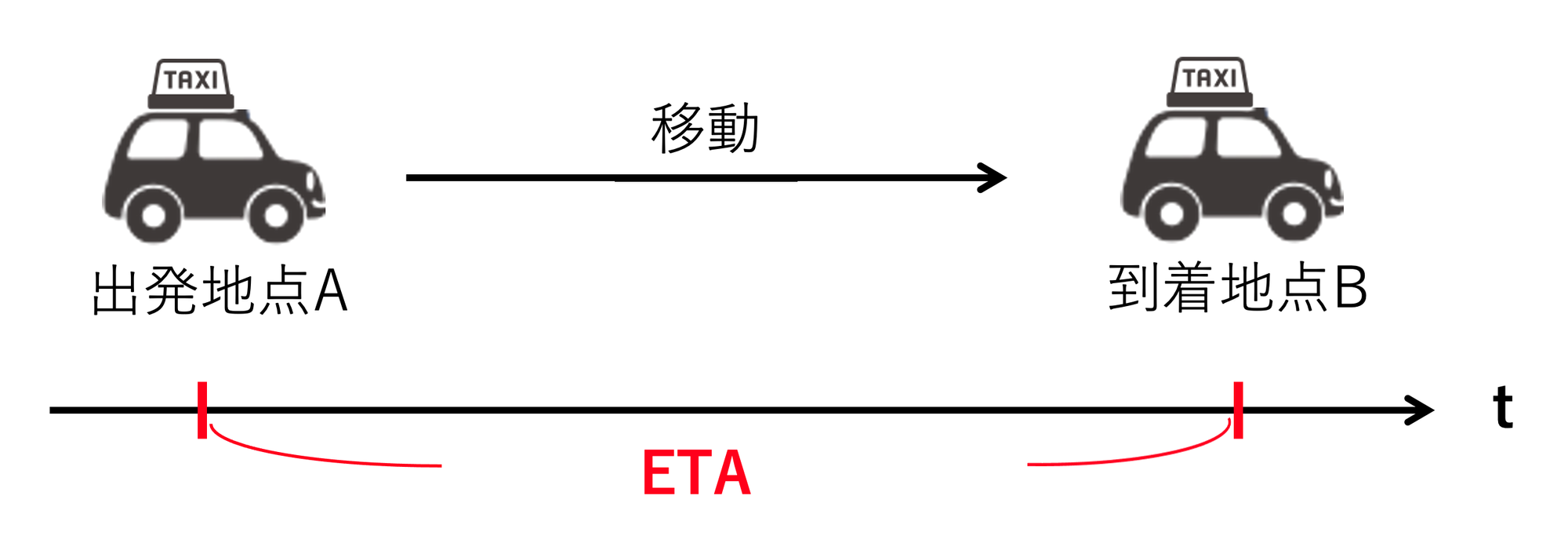
我々の運営するタクシーアプリ「GO」に限らず、カーナビなどのアプリで目的地を入力した際に表示される「XX:XX到着予定」のような時刻や、郵送物の到着時刻もETAとなり広く使われている概念となります。

どのようなところで使われているのか

そのETAですが、タクシーアプリ「GO」ではタクシーを呼ぶ画面に表示されています。

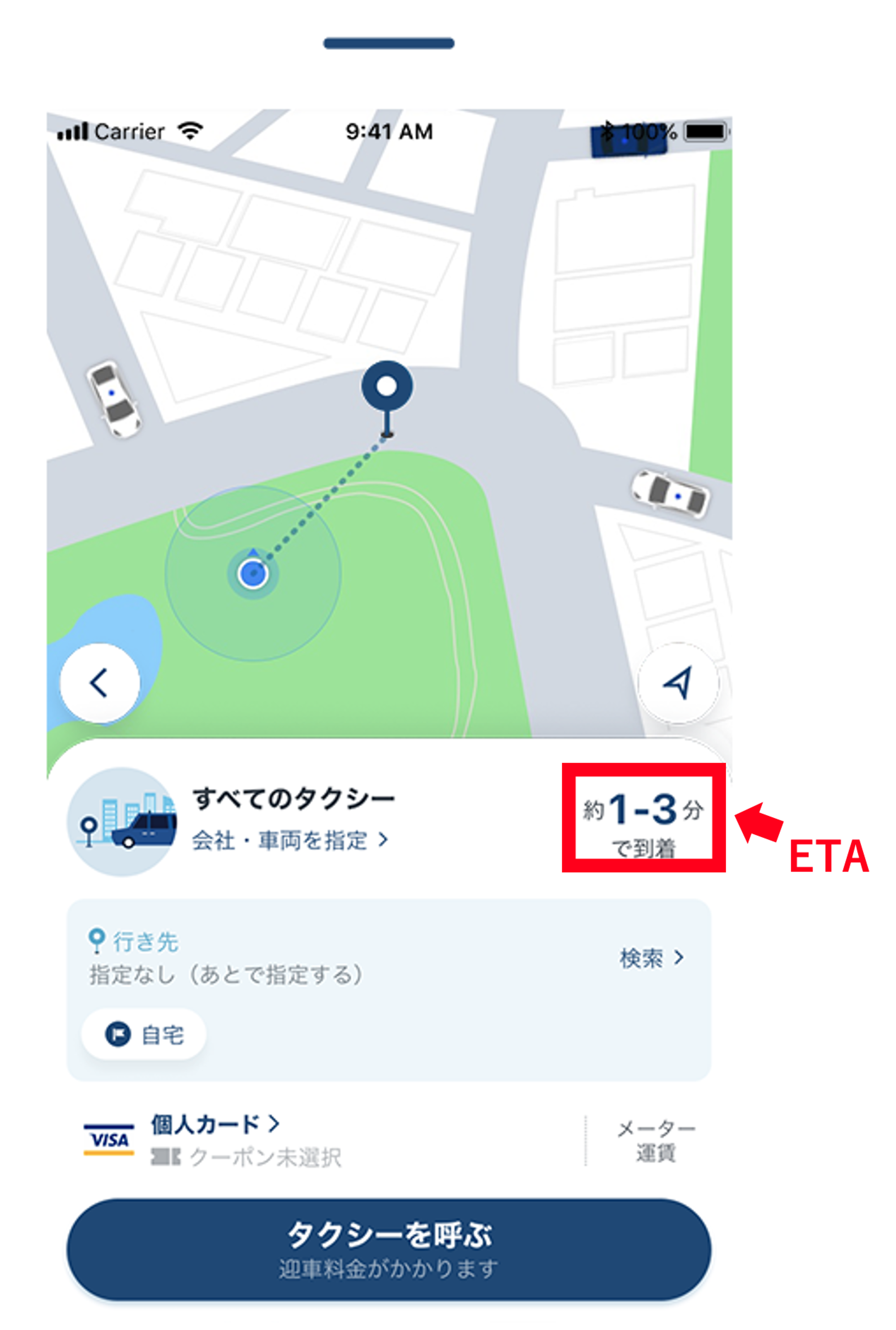
実際にタクシーを呼ぶ状況になると感じると思うのですが、

「呼んだタクシーがどれくらいの時間で到着するのか」

というETAの情報は、皆様の今後の意思決定や行動に関わる非常に重要な情報であり、実際の時間とズレてしまうことでお客様のご期待に沿えず、ご迷惑をおかけするケースが発生してしまいます。

これまでETA算出エンジンについては、外部のサービスを活用していたのですが地域や時間帯によるズレがどうしても大きかったため、内部で知見をためてより精度の高いETAの開発に成功し、順次切り替え始めております。

こちらについては、ズレの発生頻度や大きさをさらに改善するようETAの算出精度・サービス改善に継続的に取り組んでおり、本記事でもその改善の一部を紹介させていただきます。

ETA表示におけるユーザーコミュニケーションの困難さ

ETAが実際の時間とズレてしまうケースとしては、

• アプリからタクシーを呼び、実際に迎えに行く車両が確定する前後でのズレ
• 実際に迎えに行く車両が確定したあとでのズレ

の2つがありますが、本記事では前者のズレについて考えます。

(後者はリアルタイムに変化する道路状況などに大きく依存するため、さらに複雑になります)

例として、以下の2つのETAについて考えます。

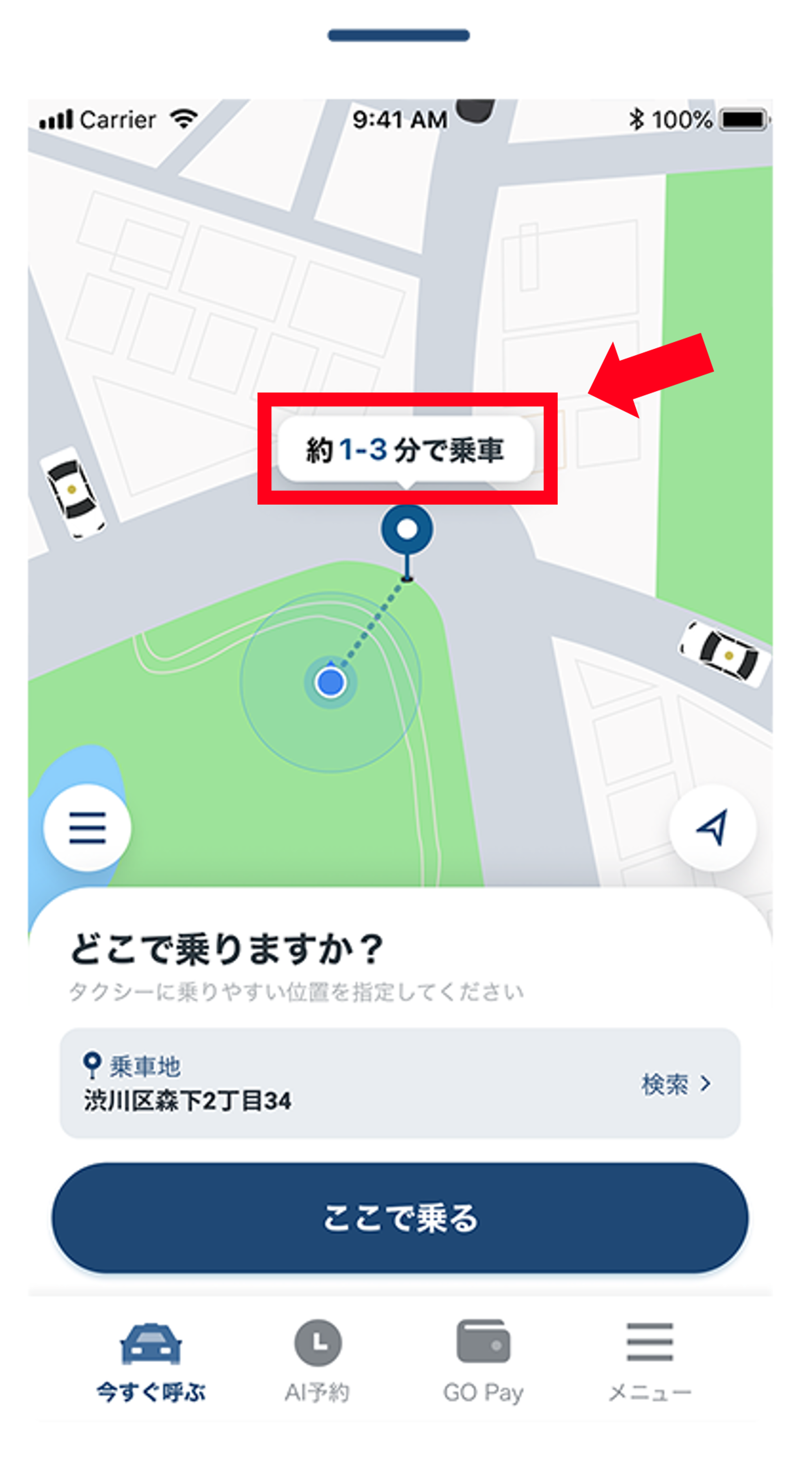
1. アプリでピンを落としたときに表示されるETA (以下、乗車までの時間)

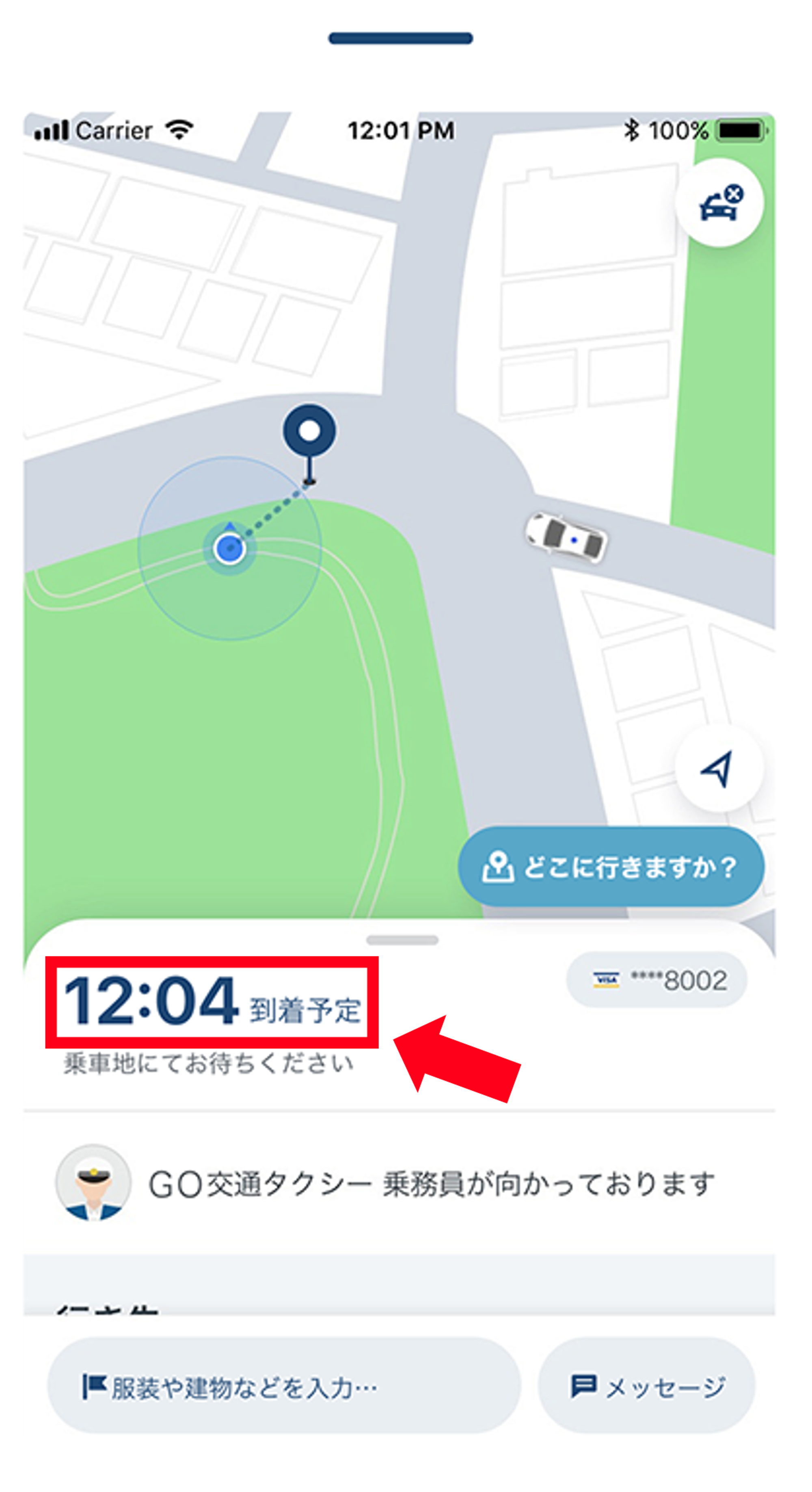
2. 「タクシーを呼ぶ」ボタンを押してから表示されるETA (以下、到着予定時間)

この2つのETAは、アプリ上の挙動としては

1. アプリを開く (乗車までの時間の表示)
2. タクシーを呼ぶボタンを押す
3. (数秒後)迎えにくる車両が決定する (到着予定時間の表示)

という3ステップで表示される値なので、ほとんど変わらない値になるはずだと思われがちなのですが、 実際にはユーザの皆様のお迎えに向かう車両の決定前後のETAのためズレが発生することがあります。

このことでお客様の期待に沿えないことがあり、大変申し訳無い事態になってしまいます。

お客様がそれでも待っていただいたのか、キャンセルされてしまうのかはお客様の判断によることもあり、単にキャンセルの有無だけでお客様に迷惑をかけたのかを測ることはできないのですが、サービス改善の１つの定量指標として、私たちはキャンセル率の変化を見ています。

今回改めてETAのズレがキャンセル率についてどう影響しているかを調査しました。

こちらの図では、

「乗車までの時間の表示」が範囲で示されるのに対し、「到着予定時間の表示」がピンポイントで時刻を表示してるので、以下のように定義して迎車リクエスト数とキャンセル率を可視化しています。

• 3分以上早着: 確定前の表示時間よりも3分以上早く表示 (乗車までの時間の下限時刻 - 到着予定時間 ≥ 3[分])
• 早着: 確定前の表示時間よりも早く表示 (乗車までの時間の下限時刻 - 到着予定時間 > 0[分])
• 範囲内: 確定前の表示時間通りに表示 (乗車までの時間の下限時刻 ≤ 到着予定時間 ≤ 乗車までの時間の上限時刻)
• 遅着: 確定前の表示時間よりも遅く表示 (乗車までの時間の上限時刻 - 到着予定時間 < 0[分])
• 3分以上遅着: 確定前の表示時間よりも3分以上遅く表示 (乗車までの時間の上限時刻 - 到着予定時間 ≤ -3[分])

※ 値はダミーですが、傾向は実際のデータと類似しています

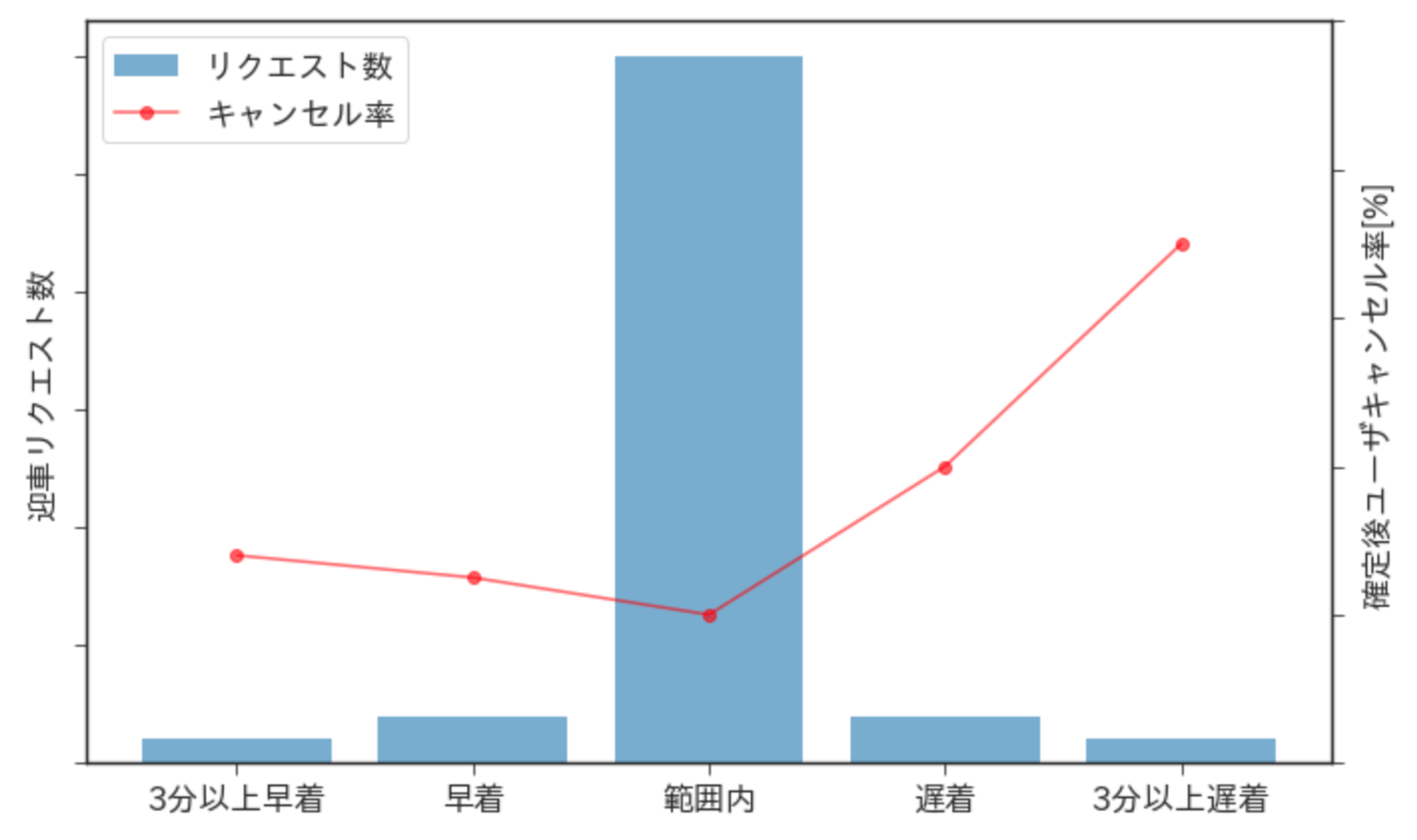
こちらの図からは、

「乗車までの時間の表示」と「到着予定時間の表示」がズレることによりキャンセル率が大きく変わること、さらに、早着と遅着を比較すると遅着方向にズレる方がキャンセル率が高くなりやすいという直感に合うような結果が観測できます。

以上のように、1つのユースケースについてのETAだけでなくユースケース別のETAとの相対的なズレも考慮しないとサービス全体にも大きな影響を与えてしまうので注意が必要です。

問い合わせ時間の微小変化に頑健なETAの算出

ETAの品質を改善するために工夫した例について1つ紹介します。

この例では以下の図のように問い合わせ時間の微小変化によって生じる「通り過ぎ問題」に対応する方法について考えます。

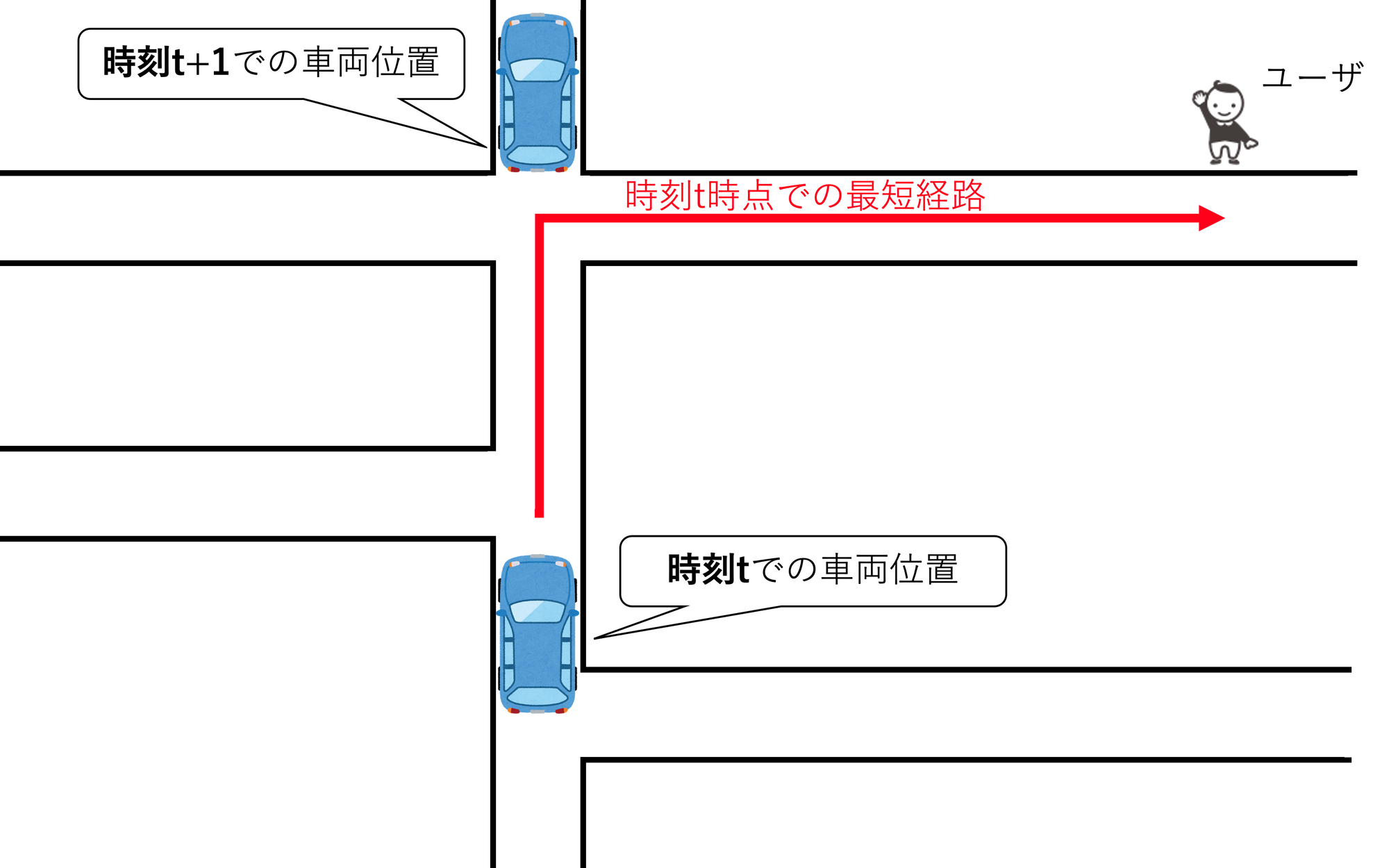
このケースでは時刻tと一定時間が経過した時刻t+1時点でのETAについて、各地点における最短経路が異なってしまうことでETAが大幅に変わってきてしまいます。

ここで生じる時刻tと時刻t+1の差分になりえる時間としては、

• 乗車までの時間を表示してから到着予定時間を表示するまでの時間 (先述のケース)
• 乗務員が配車リクエストを受け付けてから目的地を把握するまでの時間, etc.

などの時間が挙げられます。

車両が交差点近くにいる場合など、曲がる道路が少し異なってくるだけでも一方通行などの道路状況によってETAが大幅に異なってくるケースが多く存在し、この「通り過ぎ問題」を引き起こします。

この問題を解決するために道路ネットワーク上での車両移動ログから計算した時刻t+1での車両存在確率を用います。

その後、一定以上の確率で車両が存在すると推定された位置からユーザの位置までの複数の最短経路を求め、車両存在確率を重みとしたETAの加重平均を取ることで最終的なETAを算出します。

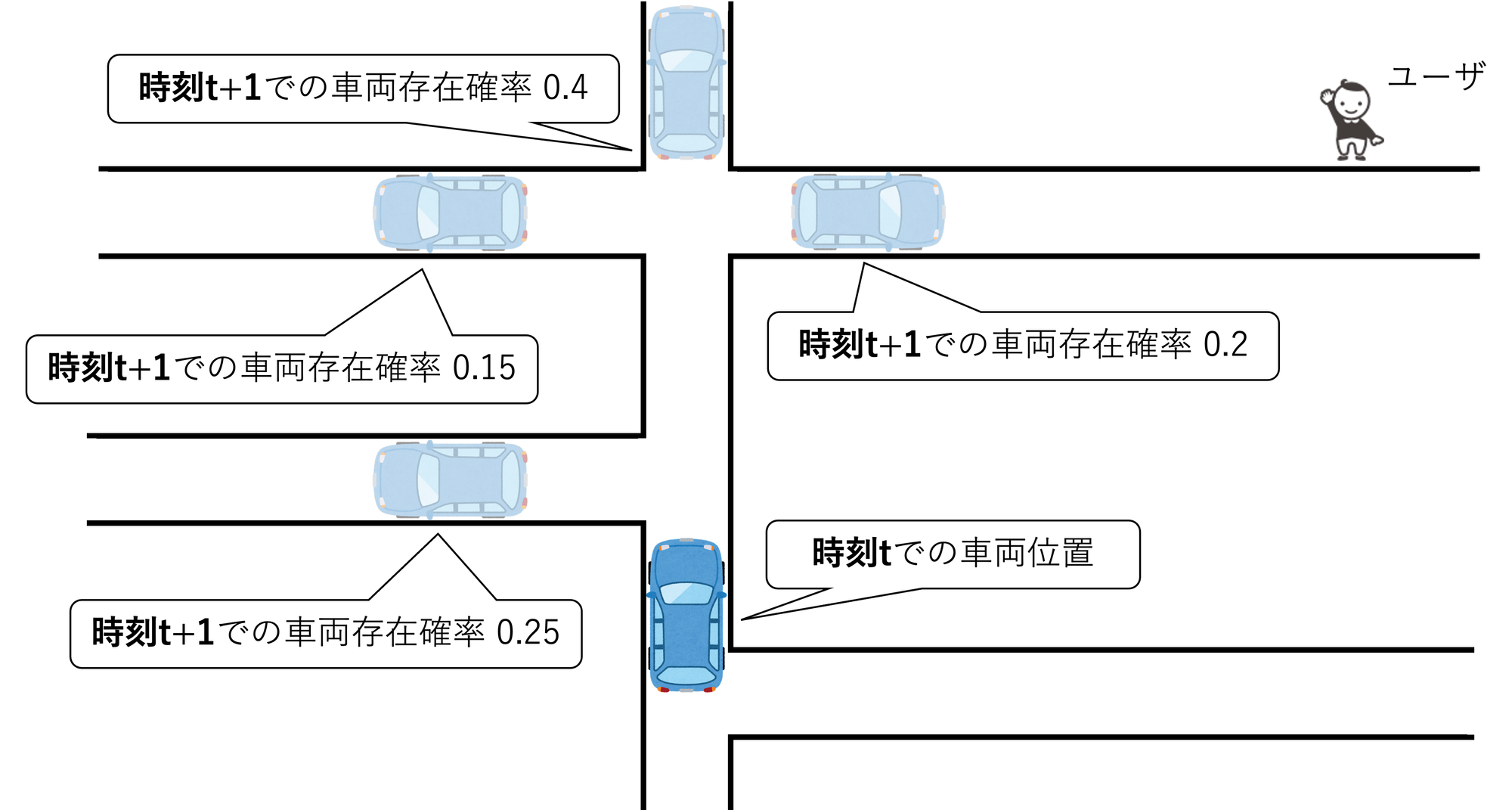
この工夫によって、「通り過ぎ問題」によるETAの変動を大幅に軽減することに成功し、現在もサービスで利用されています。

もちろんこの改善だけではまだまだ不足しており、より良いユーザー体験のために引き続きETAの改善を進めています。

おわりに

本記事では、タクシーアプリ「GO」におけるETAの使用例や品質改善のために工夫した一例を紹介させていただきました。

MoTでは他にもタクシーデリバリーアプリ「GO Dine」なども提供しており、そちらでもこのETAは利用されており、よりよいETAの算出エンジンを作るために以下のようなことを検討しています。

• 周辺車両情報から実際に迎車に向かう車両の高精度な予測
• リアルタイムな道路混雑状況の取得
• 天気やイベントなどの外部要因による道路状況の取得
• 経路探索エンジンの高速化によるレイテンシ改善
• 営業所・乗務員別の配車依頼承諾率の傾向の考慮, etc.

これらを考慮する上で、MoTとして保有する大量の配車ログデータを用いて機械学習モデルなどを検討できるのはかなりの強みでありとても楽しいです。

お客様のUXに大きく影響を与えるETAを対象とするため、解くべき問題が難しいのは間違いないのですが、乗務員・ユーザ・MoTの「全方よし」を実現するため、MoTならではのアプローチを検討し、継続的に改善を行なっていきます！

We're Hiring!

興味のある方は 採用ページ も見ていただけると嬉しいです。

Twitter @mot_techtalk のフォローもよろしくお願いします！