タクシー交通システムはどこまで効率化できるのか?
AIAlgorithmAI技術開発部アルゴリズムグループマネージャーの織田です。
MoTでは既存のタクシー交通システムのDXによる効率化を推進していますが、「果たしてどこまで効率化が可能なのか」という究極的な問いについて考えることは有益であると考えています。未来が完全に予測できるとして、最適な運行管理を行うことで無駄な走行(コスト、CO2排出量)をどの程度まで削減できるのでしょうか?本記事ではMIT Senseable City Laboのグループが提案したvehicle-shareability networkによる最小車両数問題の解法について紹介し、実際に東京のタクシートリップデータで行った評価結果について議論したいと思います。
vehicle-shareability networkによる解法
未来の不確定性が全くない場合に、その日の乗車リクエストを全てサーブするために必要な車両数を求めること(最小車両数問題)は、需要が前もってわからない現実で必要となる車両数の下限を知ることを意味します。車両数の下限を求めることができれば、例えば、サービスを展開する地域や時間帯を変更した場合に、下限値がどのように変化するかを評価でき、サービスを設計する際の意思決定にも有用です。ここでは、最小車両数問題の解法として、2018年のNature誌に掲載された論文Addressing the minimum fleet problem in on-demand urban mobilityのアプローチを紹介したいと思います。
乗車トリップ(TA,...,TF)が与えられたときの処理概要のイメージを図a~cに示します。図aは各乗車トリップの乗車地〜降車地の経路を地図上に描画したものです。色付きの矢印は、ある乗車トリップの終了(降車)から別の乗車トリップの開始(乗車)に接続できる可能性を表しています。図bは乗車トリップをノード、降車〜乗車の接続が可能なトリップの矢印を有向エッジとした有向グラフ(vehicle-sharerability network)を表しています。このネットワーク上の任意のパスは、1台の車両で連続してパス上のノードに対応する乗車トリップをサーブできることを意味します。従って、ゴールは、図cのように最小の車両数=パス数で全てのトリップをつなぐこと、つまりグラフ上のノードを全て周る最小のパス数を求めることです。
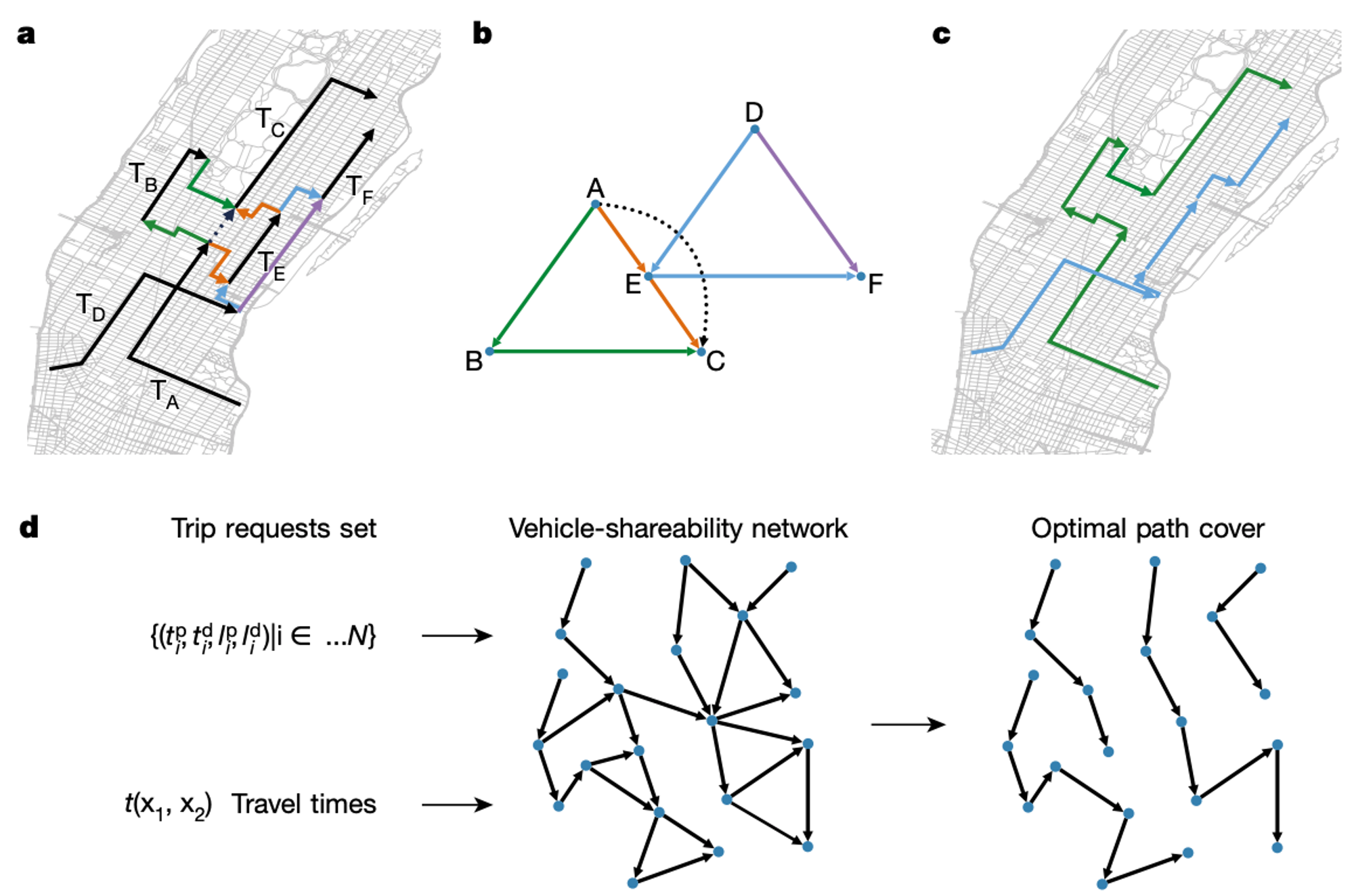
より一般的には、処理全体のフローは図dのようになります。まず、トリップ集合Tと各トリップ間の接続時間を入力として、vehicle-shareability networkが構築されます。最初のトリップの降車時刻と次のトリップの乗車時刻の差が、降車地から乗車地までの移動時間よりも長ければ、有向エッジで接続されます。また、エッジの数が増えすぎるのを防ぐため上限値を設けています()。全てのノードを周る最小のパス数を求めるminimum path cover問題は、一般的なグラフにおいてはNP困難ですが、有向非巡回グラフ(DAG)の場合は二部グラフの最大マッチングアルゴリズム(Hopcroft–Karpアルゴリズム)を用いて効率的に解けることが知られています。vehicle-sharerability networkは、時間的な制約を考えると必ず閉路のないDAG(仮に閉路が存在すると私たちはタイムスリップできることになる!)になるので、大規模なトリップデータでも最適に効率的に解くことができるのです。
東京23区のタクシートリップデータを使った実験
この論文ではニューヨーク(マンハッタン)のタクシートリップデータを用いて必要な最小車両数を評価しており、最適なスケジューリングにより、実際に稼働しているタクシー車両数から40%程度削減できると報告しています。
これはかなりインパクトのある数字だと思います。では、日本のタクシーはどうなのでしょうか?実際のデータを用いて、次のような評価を行ってみました。
- 東京23区の乗車トリップ実績データ1日分(AM5:00~翌AM5:00)を抽出する
- 降車地と次の乗車地が時間的に接続可能なトリップペアの内、時間や距離が離れ過ぎているものを除く(枝刈り)
- 残ったトリップのペアでvehicle-shareability networkを構築し、networkx.algorithms.bipartite.matching.maximum_matchingで最大マッチング問題を解く
- マッチング結果からパス(各車両のスケジュール)を復元し、30分ごとの稼働数(乗車または空車状態の車両数)と空車数を求める
この実験では素のpython実装であるnetworkxライブラリを使用しましたが、それでも23万ノード(乗車トリップ)、550万エッジのvehicle-shareability networkのマッチングが2分程度で算出できました。最適化前(実際の値)と最適化後の各時間帯における稼働数と空車数をと比較してみたのが、次の図になります。縦軸は最適化前の最大稼働数が1となるように規格化してあります。
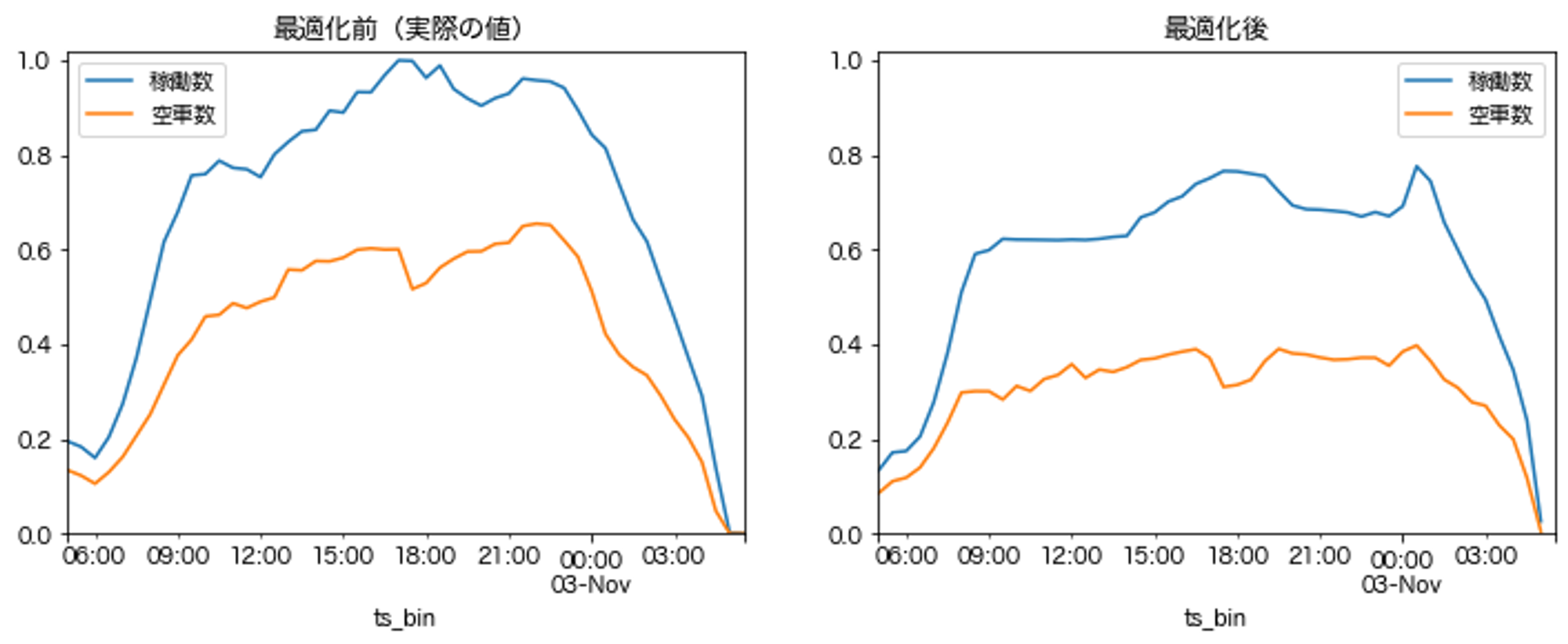
最適化により、現在の需要総量を前提に考えると理論的には稼働車両数にすると現在より20%程度少ない車両数でも対応でき、空車数は40%程度削減できることがわかりました。これは別の見方をすれば、同じ車両数でより多くの乗車トリップをサーブできるということでもあります。実際には、AI予約など事前に申し込みを行うサービスもあるものの、乗車トリップの情報を全て前もって知ることができないので、この実験結果はあくまでも理論的な限界を示したに過ぎません。現実世界での実現にはさまざまな制約が伴い、また需要急増に対するアプローチも必要になります。災害などの需要過多の際にもより多くの人が待たずに利用できるようにするためや、人材不足となっている乗務員さんの生産性を高め境遇を改善するために、どこまで効率化を目指せるかが私たちのチャレンジになります。
私たちのグループでは、現実的なタクシー交通システムの効率化を目指し、タクシー配車アプリGOのマッチングアルゴリズムやお客様探索ナビによる探客経路アルゴリズムなど、様々なアルゴリズムの研究・開発・運用を行っています。興味のある方はぜひ 採用ページ のデータサイエンティストのポジションを見ていただけると嬉しいです。
Twitter @mot_techtalk のフォローもよろしくお願いします!

