タクシー配車のマッチング・マーケットデザイン

AI技術開発部アルゴリズムグループマネージャーの織田です。

タクシーアプリ「GO」のコアとなるビジネスロジックの一つに、「利用客」と要件にあった適切な乗務員・車両（本記事では「供給者」と呼ぶ）をマッチングするアルゴリズムがあります。では、どのようなマッチングが適切なのでしょうか？近年、マーケットデザインの研究・社会実装が注目されており、モビリティプラットフォームにおいてもマーケットデザインの考え方が活用できる場面が多くあるのではないかと考えています。本記事ではタクシー配車におけるマッチング・マーケットデザインについて議論してみたいと思います。

モビリティマッチング市場

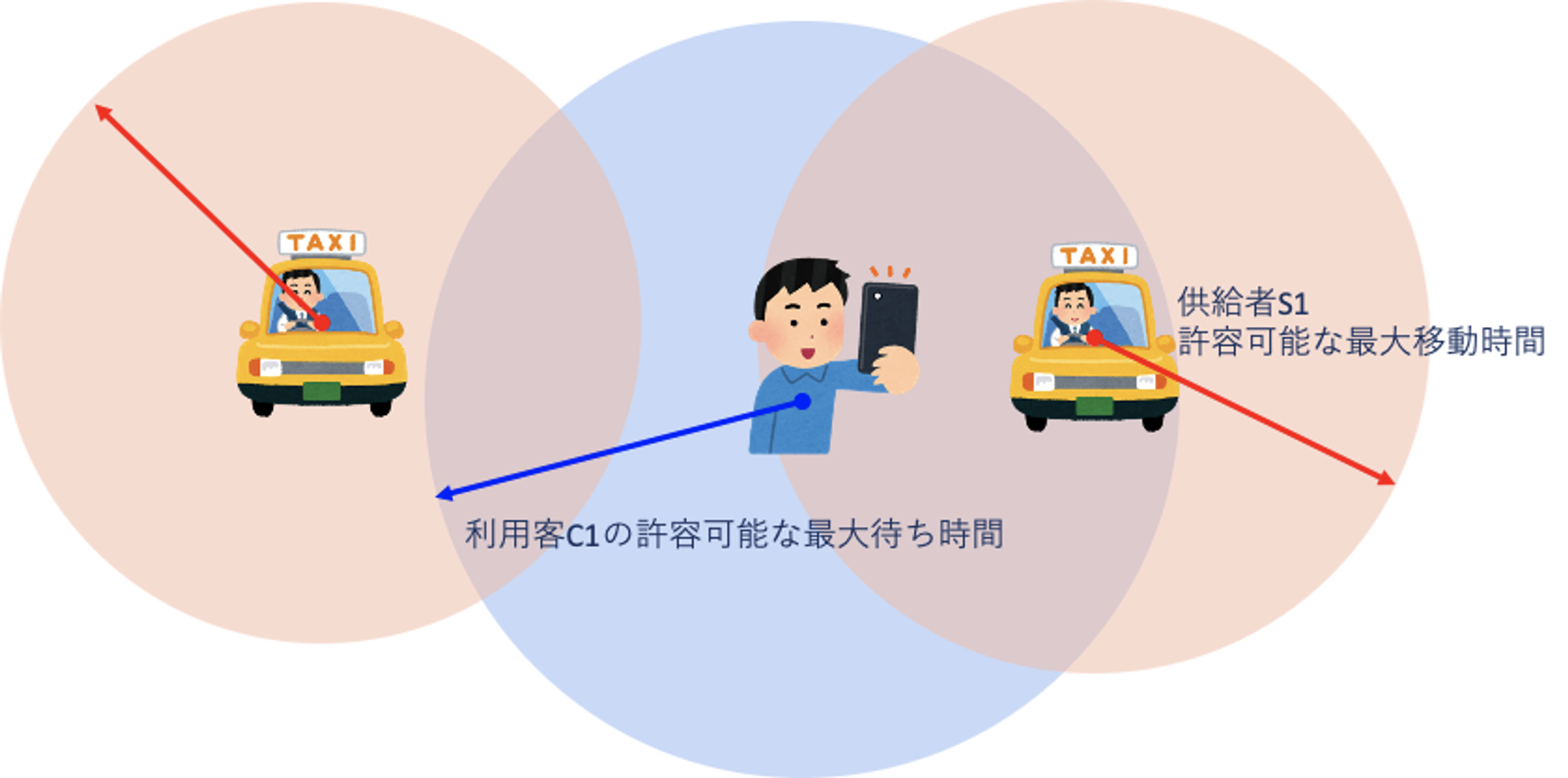
タクシー配車サービスをはじめとする多くのモビリティプラットフォームは「一対一の二部マッチング市場」と捉えることができます。ここでは、以下のような仮想モビリティプラットフォームに集まった利用客と供給者をマッチングする簡易的な問題を考えます。

• 利用客は最も待ち時間が短い供給者を好み、利用客の選好は「待ち時間が短い順の供給者」になる
• 各利用客$p$は固有の「許容可能な最大待ち時間 $w^c_p$」を持つ（この時間以上待つ供給者とマッチするくらいなら、誰ともマッチせずサービスを利用しない）
• 供給者は最も移動時間が短い利用客を好み、供給者の選好は「移動時間が短い順の利用客」になる
• 各供給者$q$は固有の「許容可能な最大移動時間 $w^s_q$」を持つ（この時間以上移動が必要な利用客とマッチするくらいなら、誰ともマッチせずサービスを利用しない

マッチングアルゴリズム

マッチングの方法は色々と考えられますが、ここでは次の３つのアプローチを検討してみます。

A. 利用客・供給者の効用最大化

経済学的には利用客と供給者の全体の効用（社会的余剰）を最大化するマッチングが良さそうです。利用客も供給者も、許容時間内であれば誰かとマッチすることでポジティブな効用を得ていると考えることができます。$\tau_{pq}$だけ移動時間が離れている利用客$p$と供給者$q$がマッチした場合、利用客の効用は$u^c_p=1-\tau_{pq}/w^c_p$、供給者の効用は$1-\tau_{pq}/w^s_q$と表せると仮定します。つまり半径を許容時間とする円の中心（待ち時間がゼロ）に近いほど効用が高く、円周上で効用0となる関数になります。

この時、効用を最大化するマッチングは、次のように得ることができます。

• 利用者と供給者をそれぞれノードとし、$\tau_{pq} < w^c_p$かつ$\tau_{pq} < w^s_q$となるノード間に重みを$u^c_p+u^s_q$とした辺をつなげた二部グラフ$G$を構築する
• $G$の最大重みマッチング問題を解く

B. マッチング数最大化・距離最小化

Aのアプローチは理想的に見えますが、いくつか問題もあります。まず、利用者や供給者が表明する許容時間に応じて１秒の価値が変わるため、不公平感があります。また、無駄な走行=エネルギー消費という観点でも最適ではありません。より公平で無駄のないマッチングはマッチング数を最大化しつつ、移動距離を最小化することで実現できそうです。つまり、アプローチAの二部グラフの辺の重みを$\lambda - \tau_{pq}$（ここで$\lambda$はマッチング数と移動距離のバランスを表すパラメータ）として最大重みマッチング問題を解くことで求めることができます。

C. 安定マッチング

上記のマッチングはいずれもバランスの取れた全体最適なマッチングを作ることができますが、マッチングが「安定」でない可能性があります。マッチングが安定であるとは、ブロックするような個人やペアがいないこと、つまり、マッチングから離脱するインセンティブを持つ個人やペアがいないことを意味します。

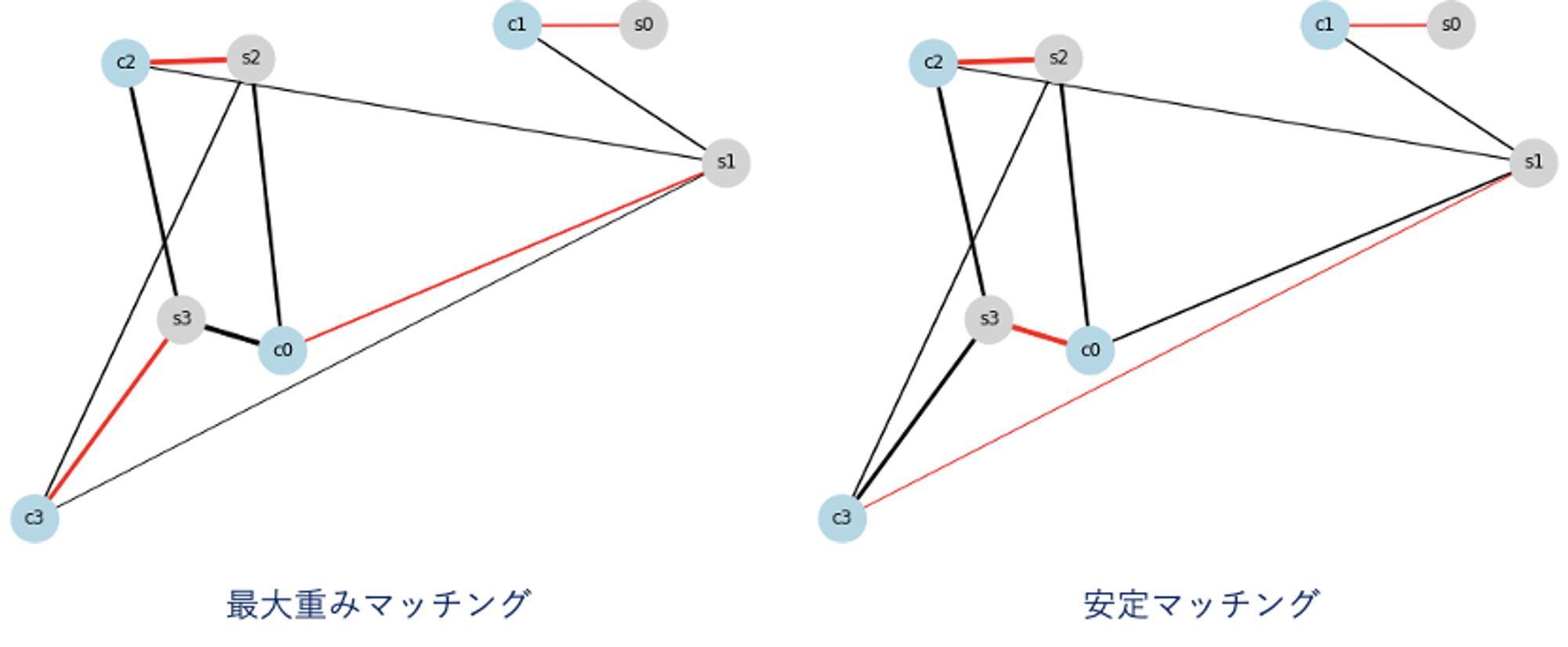
下図は利用客・供給者の位置、距離を二部グラフの位置と距離に対応させて描画したものです。効用の大きさを辺の太さでマッチングを赤線で表しています。最大重みマッチングではS3とC0は別々のペアとマッチしていますが、お互いがペアとなれば双方にとって得となるため離脱するインセンティブがあります。安定マッチングではS3とC0のペアが作られて安定的なマッチングが作られていることがわかります。

ゲールとシャプレイは1962年に安定マッチングを常に選び出すDAアルゴリズム（Deferred Acceptance Algorithm）を提案しました。利用客が提案者となる利用客側（提案）DAアルゴリズムの手続きは以下の通りです。

• それぞれの利用客が、許容可能でまだ断られていない供給者の中で、最も好ましい供給者にマッチを提案する
• 提案された供給者は、自分に提案してきた利用客と前のステップで一時的に受け入れた利用客の中で最も好ましく許容可能な利用客を一人だけ一次的に受け入れ、残りを断る
• 断られる利用客がいなくなったら終了する

利用客側DAアルゴリズムは安定マッチングの中で、利用客にとって最良となることが知られています。逆に供給者側DAアルゴリズムは、供給者にとって最良の安定マッチングとなります。

通常、利用客と供給者は全てのマッチングの情報を持っていないため、マッチングから離脱するインセンティブが働くことはないかもしれません。しかし、例えば、利用客と供給者が別の配車アプリを併用して利用している場合を考えると、別の配車アプリ上でお互いがマッチして、元のマッチングから離脱してしまう可能性は考えられます。このような状況を回避するためには「安定的なマッチング」という考え方が重要になります。

また、余談ですが、利用客側DAアルゴリズムは利用客にとって正直な選好（利用客と供給者の距離はプラットフォーム側で自動計算されるので最大許容待ち時間が該当する）の表明が支配戦略になります。つまり、利用客側には嘘をつくインセンティブがないということになります。これはDAアルゴリズムの重要な性質の一つで、利用客側耐戦略的であると言います。

実験

アルゴリズムの性質を評価するために、次のような実験を行いました。

1. ２次元空間にランダムにN人（N=5, 10, 20, 30）の利用客と供給者を発生させる
2. それぞれの利用者・供給者の許容時間を適当な分布で決める
3. アルゴリズムA, B, Cでマッチングを行い、効用（utility）、マッチング距離（distance）、マッチング率（matching_rate=マッチング数/N）、安定性（stable_rate）を評価する
4. 1~3を100回行い、各指標の平均値を算出する

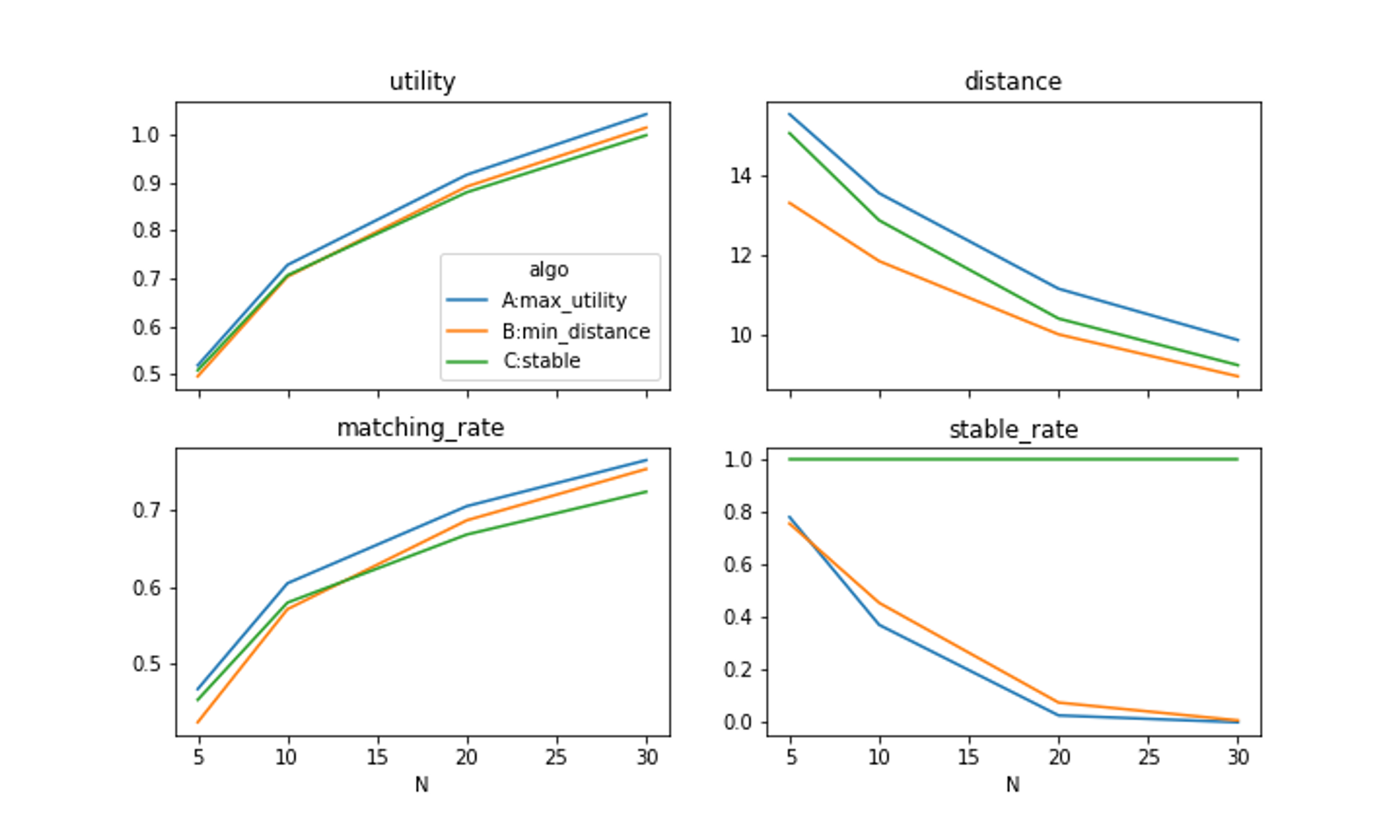
結果は以下のグラフのようになりました。想定通り、Aの効用最大化ではutilityが最大となり、Bの距離最小化ではdistanceが最小となり、Cの安定マッチングはstable_rate=1となっています。BとCを比較するとstable_rate以外は全てBが良く、安定マッチングを実現するために他の指標が犠牲となっていることがわかります。

実際のモビリティサービスに適応する場合には、アプリケーションによって重要な指標が異なるため、こういったマッチングアルゴリズムの性質をよく理解した上で、適切なメカニズムをデザインすることが必要になると思います。

We're Hiring!

興味のある方は 採用ページ も見ていただけると嬉しいです。

Twitter @mot_techtalk のフォローもよろしくお願いします！