PG BATTLE 2022参加レポート

December 06, 2022

これはMobility Technologies (MoT) アドベントカレンダー6日目の記事です。

2022年10月22日に開催された企業・学校対抗の競技プログラミング大会の PG BATTLE 2022 にMoTから参加したので、その時出題された問題・感想について記載していきます。

PG Battleとは?

PG BATTLE は年に一度行われる1チーム3人による企業・学校対抗の競技プログラミング大会で、出題されたプログラミングの問題を時間制限内に解いて提出するものです。2018年から開催されていますが、毎年1000人を超える社会人・学生が参加しています。

チーム対抗といっても、kaggleみたいに1つの問題に3人で取り組む、と言った方式でなく3人がそれぞれが「ましゅまろ」「せんべい」「かつおぶし」という難易度の問題に相談なしで取り組む方式になります。順位や勝敗は「3人が獲得した得点の合計」により順位が決まります。(同点だった場合は提出した時間が早い方が順位が上になります)

この大会は国内では有名な競技プログラミングサイトAtCoderと同様オンラインで参加することができます。利用できる言語・ライブラリがC++, Rust, PythonなどAtCoderと全く同じ環境で参加できます。AtCoderと異なる点は、大会が終了するまで自分の回答が合っているかどうかがわからずうっかりミスに気付けない点です(AtCoderでは自分の回答を提出したらすぐに合っているかどうかがわかります)。

チーム名とチームメンバー

昨年もMoTとして出場したのですが、昨年とは異なるメンバーで出場しました。(ex 昨年の参加レポート)

今年の参加メンバーは以下の通りです。

水谷亮太 (ましゅまろ)
谷本晋一 (せんべい)
亀澤諒亮 (かつおぶし)

チーム名はオーソドックスに「Team MoT」でエントリーしました。

これから、それぞれの参加メンバーから出題された問題や感想について書いていきます。

ましゅまろ

ましゅまろを担当した水谷です。AtCoderのレートは緑です。競技プログラミングは3~4年前にやっていた時期がありましたが、ここ数年は殆ど参加していませんでした。PG BATTLE には谷本さんから slack で誘われて参加しました。今回の参加者の谷本さん、亀澤さんは自分よりレートが上なので、足を引っ張らないように自分解ける範囲の問題 (レート1200以下、PG BATTLE の難易度4相当以下) は落とさないようにしようという意気込みでした。結果は3問正解という想定通りの成績で、最低限の仕事はできたかなという思いでした。

1. 難易度1「電話番号」

問題

高橋君の携帯電話番号は、090 で始まる 11 個の数字の列 $S$ で表されます。

先頭の 090 を 8190 に置き換えることで、電話番号を国際電話用に変えることができます。

高橋君の携帯電話番号を国際電話用に変えてあげてください。

制約

$S$ は 0 から 9 の数字のみからなる長さ 11 の文字列
$S$ は 090 から始まる

解法

090を8190に置換すればOKです。文字列長が固定かつケースが限定されており、初心者であっても1問は正解させてあげたいという運営の意志を感じました。

2. 難易度2 「等式」

問題

$N+1$ 個の整数と $N$ 個の記号( $+$ または $=$ )からなる数式 $a_{1} \ op_{1} \ a_{2} \ op_{2} … op_{N} \ a _{N+1}$ が与えられます。この数式が正しいかどうか、すなわち $=$ で結ばれた式がそれぞれ等しいかを判定してください。

制約

$1 ≤ N ≤ 100$
$1 ≤ a ≤ 100$
$N,a_{i}$ は整数
$op_{i}$ は $+$ または $=$
$op_{1},..., op_{M}$ に $=$ が少なくとも1つ含まれる

解法

$=$ で分割された $a_{i}$ と $+$ で構成されたグループを作り、各グループの $a_{i}$ の和が同じであることを確認できればOKです。

3. 難易度3 「試験の成績」

問題

人1, 人2,..., 人 $N$ の $N$ 人が試験を受けました。

試験は数学と英語の2科目からなります。人 $i$ は数学で $a_{i}$ 点英語で $b_{i}$ 点を取りました。

試験の成績は数学と英語の点数の重み付き和によって決まります。具体的には、人の総合成績を $p * a_{i} + q * b_{i}$ と定義します。( $p,q$ は正の整数)

人 $i$ の順位を(人 $i$ よりも総合成績が真に高い人の人数) +1 と定義します。

人1の順位, 人2の順位,..., 人 $N$ の順位を順番に出力してください。

制約

1 ≤ $N$ ≤ 2 x $10^5$
1 ≤ $a_{i}$ , $b_{i}$ ≤ $10^{4}$
1 ≤ $p$ , $g$ ≤ $10^4$
入力される値はすべて整数

解法

まずすべての人に対して得点を算出し、得点順でソートして順位をつけます。このとき元の順番は保持しておきます。次に元の人の並び方に戻してあげればOKです。同じ得点の場合は同じ順位になりますが、ソートするだけだとそうならないので、そこは気をつける必要がありました。

4. 難易度5 「沈黙」

問題

$N$ 杯の蟹があります。各蟹は10本の脚と1単位の蟹味噌で構成されています。 $i = 1,..., N$ に対し、 $i$ 番目の蟹の脚1 本の美味しさは $a_{i}$ 蟹味噌1単位の美味しさは $b_{i}$ です。

高橋君と青木君はこれらの蟹を以下の条件を満たすように分け合うことにしました。

どの1本の脚及びどの1単位の蟹味噌もどちらか一方に分けられる
「高橋君に分けられた脚と蟹味噌の美味しさの総和」と「青木君に分けられた脚と蟹味噌の美味しさの総和」は等しい

条件を満たす分け方が何通りかを 998244353で割った余りを求めてください。

ただし、ある2つの分け方は、ある1本の脚またはある1単位の蟹味噌であって、一方の分け方では高橋君に、もう一方の分け方では青木君に分けられているようなものが存在する場合に区別します。脚同士や蟹味噌同士はたとえ美味しさが等しくても区別されることに注意してください。

制約

1 ≤ $N$ ≤ 8
0 ≤ $a_{i}, b_{i}$ ≤ $10^{15}$
入力は全て整数

解法

これは解けませんでした。本番で考えていたこととしては、1杯の蟹の分割パターンは $2^{11}$ で全列挙できるのでそれで条件に合う方法が探索でき、 $N$ 杯の分け方を独立と考えるとそれぞれの結果を掛け算すれば良いという方針でした。しかし、これだとサンプルケースは通りますが、 $N$ 杯の分け方は独立でない(それぞれの杯で考えると条件に合わないが、合わせると条件にあうケースが存在する)ので不正解です。

正解の解法ですが、まず分割パターンを工夫して減らす必要があります。同じ杯の脚の価値は同じなので、高橋くんと青木くんが杯の中身をいくつずつ分け合うかは11通り、どちらが味噌を持つかが2通り、 $N$ が最大で8なので、パターン数を $22^8$ とすることができます。ただこれでも制限時間に間に合いません。この問題では全体の総数は決まっているので高橋くんの方だけ見て値が合計値の半分の値になれば条件に合うことがわかります。すると探索範囲を2つのグループに分割する半分全列挙という手法が使用でき、結果パターン数を $22^4$ に減らせます。最後に、各パターンについて合計値が全体の半分に該当するか、該当する場合はそのパターンに対応する組み合わせが何通りあるか(例：高橋くんが脚を8本と味噌1個、青木君が脚2本と分けた場合、脚の分け方は ${}_{10}C_{2} = 45$ )を考えることで、分け方の総数を制限時間内で算出することができます。

感想

PG BATTLE は個人が別の問題を解く形式なのでチーム戦の要素は少ないのですが、解けないとチームとしての合計点が下がるため、普段一人で参加する時よりも緊張感があってよかったです。また、PG BATTLE の特徴として提出は一度のみという制約があるのですが、これも個人的には好きな要素でした。AtCoder だと提出が間違っていても時間にペナルティがかかるだけで再提出可能なので、こんな感じで通るかな？という確信度で提出することも少なくないです。しかし実務よりのことを考えると、確定前に想定されるケースを洗い出しておくことは重要なので、そういうことを考える練習にもなって良いかなと思いました。自分は今はアルゴリズムよりもヒューリスティックと呼ばれる長時間で1問を解く形式のコンテストに興味があるのですが、そちらでも複数人で1問の共通の問題を解く団体戦があっても面白そうかなと思いました。

せんべい

せんべいを担当した谷本です。去年の10月あたりからAtCoderのプログラミングコンテストに積極的に参加し始めており、大会出場当時のレートは水色です(執筆している2022/12/4時点で青色にななっています)PG BATTLEは今回が初参加になります。

本番では別々に問題を解く、と言ってもやはりチームなので本番までに週1の90分間チームで練習してきました。AtCoderの過去問を使った練習や運営から提供されたPG BATTLEの過去問を使って練習してきました。これまでは自分一人で練習してきましたが、チームで練習することで「バグりにくいコードの書き方」をお互いに共有できたのはよかったと考えています。

肝心な本番ですが、4問中2問正解でした。練習では4問中3問解くとかできてたんですが、ケアレスミスで1問ロスしてしまいました。

1. 難易度2「せんべい」

問題

$N$ 枚のせんべいが一列に並んでいます。全てのせんべいは表裏が区別できます。全てのせんべいははじめ表を向いています。

あなたは $Q$ 回の操作をします。 $i$ 回目の操作では、左から $L_i$ 番目から $R_i$ 番目までのせんべいを裏返します。(裏を向いているせんべいを裏返すと表を向いた状態になるのに注意してください。)

$Q$ 回の操作を全て終えた後に裏を向いているせんべいは何枚ありますか？

制約

$1≤N≤100$
$1 \leq Q \leq 100$
$1 \leq L_i \leq R_i \leq N$
入力される値はすべて整数

解法

長さ $N$ のbool型の配列を用意して、素直に $i$ 回目の操作では、 $L_i$ 番目から $R_i$ 番目まで要素のbool値を逆転させていきます。最後に「裏」に対応するbool値の要素数を数えておしまいです。

いきなり難しい問題でなく最初はこういう簡単な問題でウォーミングアップできるのもPG BATTLEのよさでもあります。

2. 難易度3「食品の区別」

問題

ここに、 $1,2,\dots,3N$ の番号がついた $3N$ 個の食品があります。 $i$ 番の食品の固さは $A_i$ であり、全ての食品の固さは互いに異なることが分かっています。加えて、以下のことも分かっています。

この中に「ましゅまろ」「せんべい」「かつおぶし」がちょうど $N$ 個ずつある。
どの「せんべい」も、どの「ましゅまろ」より固さが大きい。
どの「かつおぶし」も、どの「せんべい」より固さが大きい。

食品のうち「せんべい」であるものの番号を求め、昇順に出力してください。なお、答えが一意に定まることが証明できます。

制約

入力はすべて整数
$1 \le N \le 10^5$
$1 \le A_i \le 10^9$
$A_i$ は相異なる

解法

問題文をよく読むと「 $3N$ 個の食品の中で $N+1$ 番目~ $2N$ 番目に固い食品がせんべいである」ということがわかります。なので、 $3N$ 個の食品を固さで昇順ソートし、 $N+1$ 番目~ $2N$ 番目の要素を抜き出せた配列を出力すればOKです。

ただし、答えを出力する際に番号が昇順になっている必要があるので、抜き出した後の長さ $N$ の配列を番号について昇順にソートして出力する必要があります。

3. 難易度4「区間の削除」

問題

長さ $N$ の正整数列 $A = (A_1, A_2, \ldots, A_N)$ が与えられます。

$A$ に対して、次の操作を好きなだけ（ $0$ 回でも良い）繰り返します。

まず、 $1 \leq l \leq r\leq N$ を満たす整数 $l, r$ であって、 $(A_l, A_{l+1}, \ldots, A_r) = (1, 2, \ldots, r-l+1)$ であるものを選ぶ。
そして、 $A$ から $A_l, A_{l+1}, \ldots, A_r$ を削除する。その結果、 $A$ は元より長さが $r-l+1$ だけ短い列 $(A_1, A_2, \ldots, A_{l-1}, A_{r+1}, A_{r+2}, \ldots, A_N)$ へと変化する。

最終的な $A$ の要素の和としてあり得る最小値を出力してください。ただし、最終的な $A$ の長さが $0$ の場合、要素の和は $0$ とみなします。

制約

$1≤N≤5×10^5$
$1 \leq A_i \leq N$
入力はすべて整数

解法

まず、stackを用意します。数列 $A$ の一番後ろの要素からstackに詰めいき、 $1$ をstackに詰めるタイミングで「 $1, 2, 3, 4, …, n$ 」の連続した値の部分だけ stack からその部分を除く、という取り除き方が、求める最小値を出すための方法になります。数列 $A$ の要素を全て見ていった後、最後にstackの中にある要素の和が求める最小値になります。

この方法での計算量は $O(N)$ になるので十分実行制限時間に間に合います。

このようにアプローチ自体は合っていたんですが、コーナーケースの処理でコーディングミスをしてしまい、不正解になってしまいました。

4. 難易度6「都市の合併」

(問題文があまりに長すぎたので本質的な部分だけ抜き出しました。そのため問題のタイトルと噛み合っていないように見えますがご了承ください。問題文全て見たい場合はこちら。)

問題

$N$ 頂点の無向木 $T$ があり、頂点 $i$ には整数 $a_i$ が書かれています。頂点の集合 $S$ のスコア $F(S)$ を次のように定めます。

$T$ の $S$ に対する誘導部分グラフが連結である場合は $F(S) = \sum_{c \in S} a_c$
そうでない場合は $F(S) = 0$

$c=1, 2, \dots, N$ について次の式を計算してください。

$\displaystyle \left(\sum_{S \subseteq\lbrace 1,2,\dots,N\rbrace, \;c \in S} F(S)^K\right) \bmod{998244353}$

制約

$2≤N≤1000$
$1 \leq K \leq 50$
$1 \leq a_i \leq 10^8$
$1 \leq A_i, B_i \leq N$
すべての都市は互いに行き来できる
入力される値はすべて整数

解法

この問題はtwitterのタイムラインでも「鋼鉄せんべい」と揶揄されていたぐらいかなり難しかったです。

正解の解法はこのブログで伝えようとすると膨大な量になるためここではキーとなる用語だけ紹介します。詳細な解説は公式解説動画をご覧ください。

木構造に対する全方位木dp
convolution ( $K$ 乗の項を帰納的に解くためのテクニック)
数列 $A$ から $1$ つの要素を取り除いた集合に対する $K$ 乗の項の効率的な計算

全方位木dpを使うところとconvolutionというところは思いついて実装しようとしたが、実装が間に合わず提出すらできずに終了してしまいました。(3. については思いつきもしませんでした。)

感想

普段取り組んでいるAtCoderのコンテストと違い、「コンテスト中にケアレスミスに気づいて修正する」ということができないので、いつもより緊張感を以って取り組むことができました。結果的にケアレスミスしてしまい足を引っ張ってしまったのですが、「チームでプログラミングコンテストに出て戦績を残す」という点では達成できたのではないかと思います。

企業の部で出場したチームは188チームだったのですが、その中で38位というまずまずな成績を収めました。結果発表の際に上位10チームも発表されるのですが、点数だけでいくとケアレスミスさえなければもう少し善戦できてたのでは？と考えています。

次回、MoTでチームとして出場する際は、ケアレスミスを絶対にしないような練習とかを取り入れて臨みたいです。

かつおぶし

かつおぶしを担当した亀澤です。今回PG BATTLEへの参加は4回目になります。いずれもかつおぶしを担当してきて今年こそ全完と思っていたんですが、結果としては1問目「等差数列」と3問目「模様」の2完で終わってしまいました。簡単に解法を説明します。また、Rust実装でのACコードはこちらです。

1. 難易度3「等差数列」

問題概要

項数 $N+1$ で公差が正の等差数列 $A=(a_1, …, a_{N+1})$ が隠されています。 $A$ から $a_1$ と $a_{N+1}$ 以外の1項を除いた残りの $N$ 項が順不同で $B=(b_1, …, b_{N})$ として与えられるので取り除かれた項を求めてください。

制約

$2 \le N \le 1000$
$1 \le b_i \le 10^9$
$B$ は問題文中の記述と矛盾しない

解法

まず $N=2$ の場合、取り除かれた項は $a_2$ になります。したがって、 $b_1$ と $b_2$ の平均が答えになります。

$N \ge 3$ の場合、公差を求めることで $B$ に含まれない項を見つけることができます。公差は、 $B$ をソート後に隣り合う項の差分の最小値となり、 $B$ の最大値以外の各項に公差を足した値が $B$ に含まれていない場合、それが答えになります。

2. 難易度4 「反射」

問題概要

平面上に $(0, 0), (W, 0), (W, H), (0, H)$ を頂点とする長方形の壁があります。長方形内部の始点 $(sx, sy)$ から時刻 $0$ に $x$ 軸正の向きから $a$ 度回転した向きに速さ1で等速直線運動し、壁に達するたびに鏡面反射します。時刻 $T$ に長方形内部の終点 $(tx, ty)$ に到達するような実数 $a \; (0 \le a < 360)$ の選び方が何通りあるか求めてください。

制約

$2 \le W, H \le 2 \times 10^5$
$1 \le sx, tx \le W-1$
$1 \le sy, ty \le H-1$
$1 \le T \le 2 \times 10^5$

解法

鏡面反射は折り返しと考えることで、折り返しを広げることで直進のみを考えればよくなります。今回の問題の場合、長方形とその内部の始点と終点を折り返したグリッドを考えることとします。具体的には下のような図を考えます（簡単のために一部の線のみ書いています）。

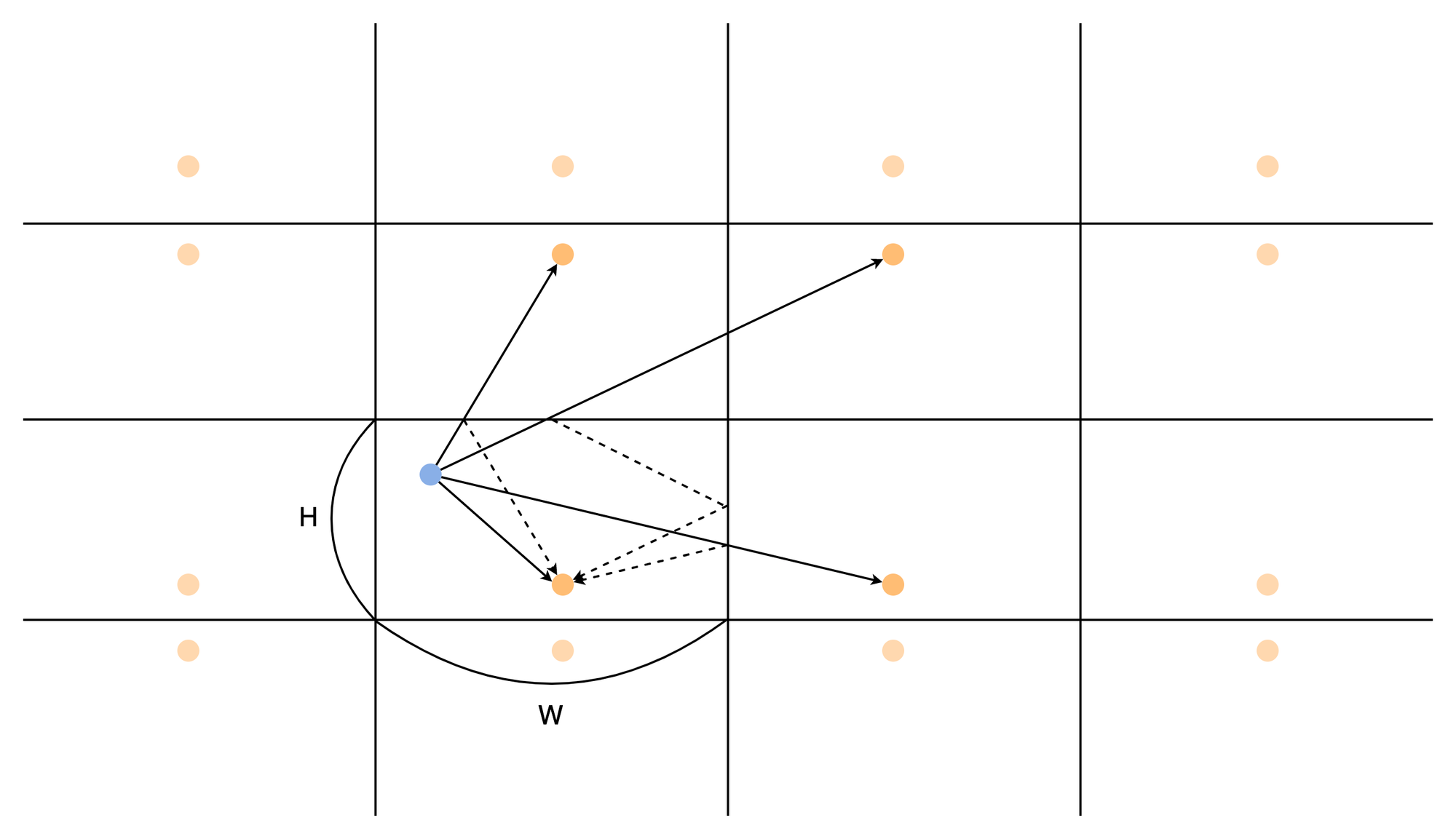
このように考えると、進む向きとして実数 $a$ の代わりに折り返された終点の座標を選べば良いことになります。したがって始点から各グリッドの終点までの距離が $T$ となるようなグリッドの個数を数える問題になりました。x軸方向のグリッドの位置を固定すると、距離が $T$ となるような終点を含むグリッドがあるかどうか定数時間で判定できるため、計算量は $O(T)$ となります。実装上は終点の位置が上下左右に反転した4種類のグリッドを考慮する必要があるので符号などに注意が必要です。

3. 難易度5 「模様」

問題概要

$N$ 行 $M$ 列のグリッド $A$ （ $i$ 行 $j$ 列目のマスが $A_{i,j}$ ）があり、各マスには0, 1のどちらかを書き込むことができます。0, 1からなる長さ $N$ の文字列 $S$ と長さ $M$ の文字列 $T$ から $A$ の各マスの値は次のように定められています。

$A_{i, 1} = S_i$
$A_{1, j} = T_j$
$A_{i, j} = A_{i, j-1} \oplus A_{i-1, j}$ （ $i,j \ge 2$ , $\oplus$ は排他的論理和）

$K$ 個の整数組 $(X_i, Y_i)$ について、 $A_{X_i, Y_i}$ に書き込まれている値を求めてください。

制約

$2 \le N, M \le 2 \times 10^5$
$S_1 = T_1$
$1 \le K \le 10$
$1 \le X_i \le N$
$1 \le Y_i \le M$

解法

愚直に $A$ を求めると計算量は $O(NM)$ になり、この制約では間に合わないため、工夫が必要になります。今回の場合、 $K$ が十分に小さいため、 $A$ の全てのグリッドではなく、与えられたグリッドのみ計算する方法を考えます。グリッド $A_{i, j} \;(i, j \ge 2)$ に対する $S$ , $T$ の直接の寄与を考えると二項係数を用いて次のように表すことができます（これはグリッド上を右か下に移動する場合の経路数と等価になります）。

A_{i, j} = \left(\bigoplus_{2 \le k \le i} \binom{i-k+j-2}{i-k} S_k\right) \oplus \left( \bigoplus_{2 \le k \le j} \binom{i-2+j-k}{j-k} T_k \right)

あとは二項係数の計算についてですが、階乗について予め計算しておく（計算量 $O(N+M)$ ）とそれぞれ定数時間で計算できます。また、今回は mod 2 での値さえわかれば良いのでLucasの定理を用いることで前計算なしで直接で求めることもできます（実装は公式解答例を参照）。

4. 難易度6「二歩」

問題概要

$N \times N$ のグリッドがあり、上から $i$ 行目、左から $j$ 列目のマスをマス $(i,j)$ と呼びます。各マスは黒または白の色がついていて、マス( $i,j)$ の色は $S_{i, j}$ として与えられます。このグリッドに以下の制約のもと、0個以上の駒を置くことができます。

黒いマスに駒をおいてはいけない
全てのマスについて、置くことのできる駒は1個以下
同じ列に駒を複数置いてはいけない

0個以上の駒を置いた後のグリッドに対して、次のようにスコアを定義します。

$i$ 行目に置かれている駒の数を $A_i$ として、 $\operatorname{max}_{1\le i\le N} A_i$

考えられる全ての駒の置き方に対してスコアの総和を998244353で割った余りを求めてください。

制約

$1 \le N \le 13$

解法

これも考えられうる全ての駒の置き方は膨大（ $O(N!)$ , $N=13$ の場合、およそ $6\times 10^9$ ）になるため、ナイーブに求めることは難しいです。この問題では動的計画法（DP, Dynamic Programming）、特にビットDPと言われる方法を用いることで効率的に解くことができます。具体的には、「上から $i$ 行目までみたときに、各列にすでに駒が置かれているかどうか表すビット配列が $S$ で、スコアが $X$ となっているような駒の置き方の総和」 $\text{dp}[i][S][X]$ を考えます。次の行にどの列に駒を置くかという遷移を考えると配るDPの要領で場合の数を足していけばDPテーブルを埋めることができます。このDPテーブルを使うことで、最終的な答えを $\sum_{X=0}^N X \times \text{dp}[N][(1<<N)-1][X]$ と求めることができます。

ただし、このDPをナイーブに実装すると $O(N^24^N)$ となるため、制限時間に間に合いません。すでに駒が置かれた列には新たに駒を置けないという条件から全ての駒の置き方の遷移を行う必要はなく、実は $O(N^2 3^N)$ で実装することができて、この計算量なら制限時間に間に合います。3乗という数字は各列ですでに駒が置かれたかどうかと、新たに駒を置くかどうか、の4通りの組み合わせのうち、すでに駒が置かれていて、かつ新たに駒をおく、というパターンを考える必要がないため、残りの3パターンだけの遷移を考えればよいことから導けます。

感想

冷静に時間をかければ解けるような問題が多く、考察、実装の速度が求められるような問題セットになっていたと思います。2問目は単純に考察ミス、4問目は時間が足りずに解くことができませんでした。ただ、今回PG BATTTLEに向けてチームで練習する中で、フィードバックがなくてもミスをしないような意識や、実装上の工夫はチームで身につけることができたのではないかと思います。

最後に、明日のMobility Technologies アドベントカレンダー 7日目は大西哲也さんによる「MoTに入社して半年のデザイナーが語る会社の率直な感想と今後」です。お楽しみに！

We're Hiring!

📢

Mobility Technologies ではともに働くエンジニアを募集しています。

興味のある方は採用ページも見ていただけると嬉しいです。

Twitter @mot_techtalk のフォローもよろしくお願いします！