因果推論における変数選択
AIAI技術開発部分析グループの島田です。 分析グループは、タクシーアプリ「GO」におけるデータドリブンなビジネス意思決定を行うために、様々なユーザ分析、乗務員分析を行っています。 今回は因果推論における変数選択の役割について紹介します。
機械学習における変数選択
まずは、機械学習ライブラリのscikit-learnに実装されている変数選択(feature_selection)の説明を見てみましょう。
The classes in the sklearn.feature_selection module can be used for feature selection/dimensionality reduction on sample sets, either to improve estimators’ accuracy scores or to boost their performance on very high-dimensional datasets.
scikit-learnの説明によると、変数選択は「正解率の向上」と「高次元データでのパフォーマンス向上」のために使うものであるとなっています。
しかし、機械学習に慣れている方からすると、「正解率の向上」について言えば、変数選択によるノイズ除去よりも情報量の減少による性能低下が気になりますし、ノイズ混じりの変数であってもDNNやRandom Forestはモデル内で対処可能だと考えると思います。
また、「高次元データでのパフォーマンス向上」のために変数選択をするのは、計算機資源が乏しかった過去の話で、今ではパフォーマンスが出ないということであれば、クラウドで計算機資源を投入するという選択があるので、変数選択を使うことは少ないと思います。
変数選択が必要な場合
では、どのような場合に変数選択が必要になるのでしょうか?
一例として、Evidence on the impact of sustained exposure to air pollution on life expectancy from China’s Huai River policyでの議論を取り上げてみたいと思います。
論文中では、中国の北部で行われた大気汚染対策の効果を、南北それぞれの平均寿命推定モデルの差とする回帰不連続デザイン(RDD)で推定しています。
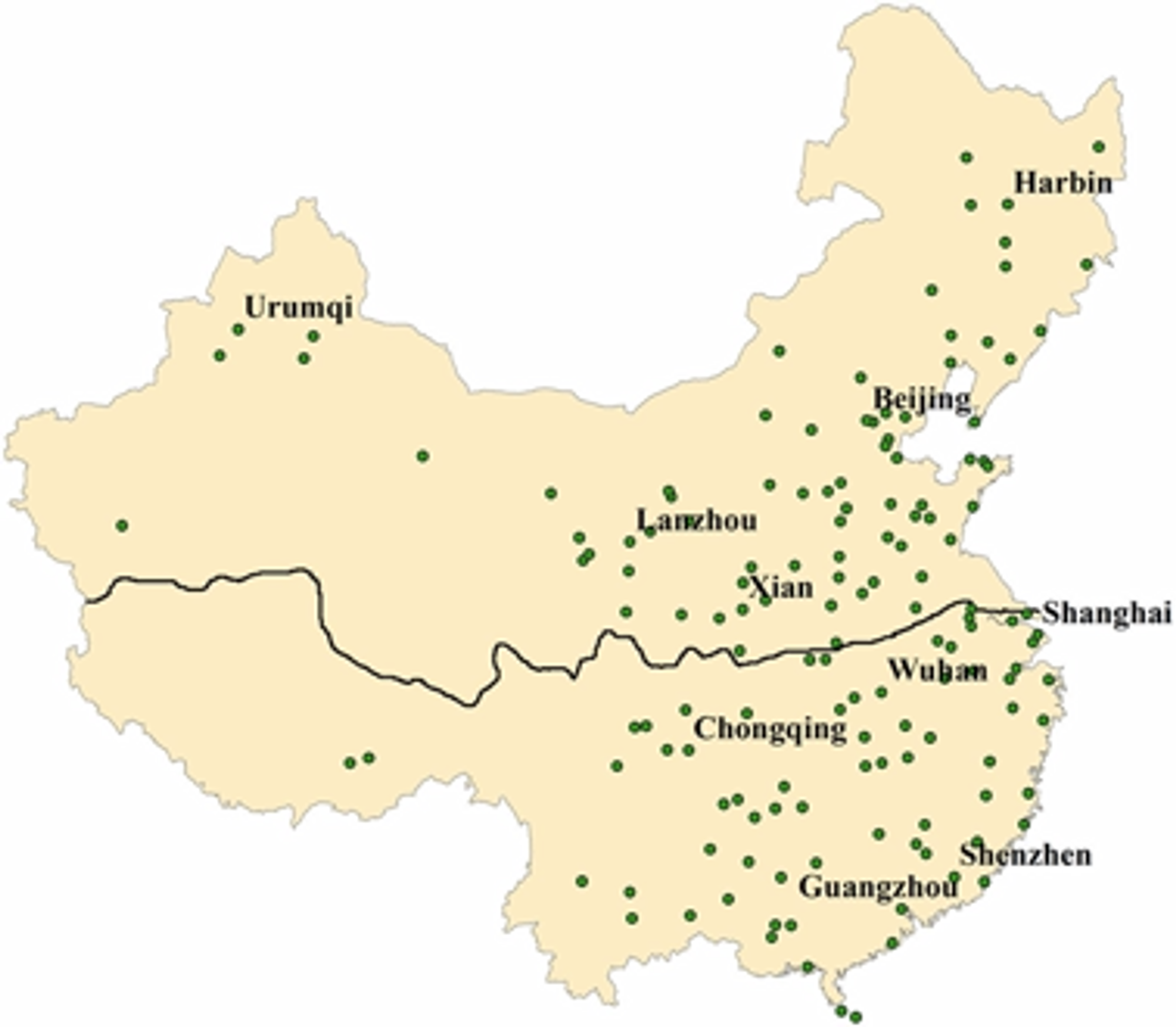
淮河(黒線)の北側で大気汚染対策が行われた
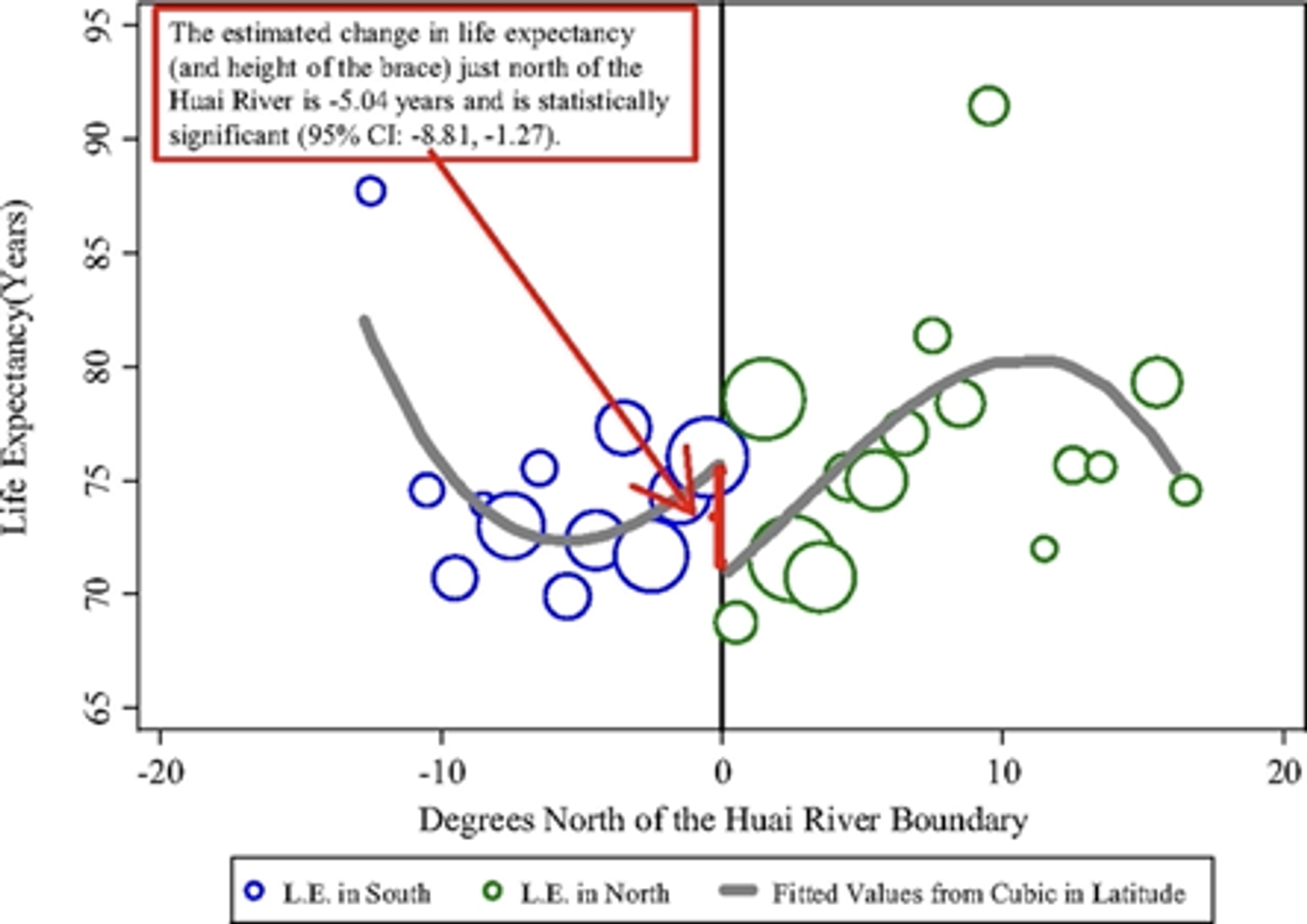
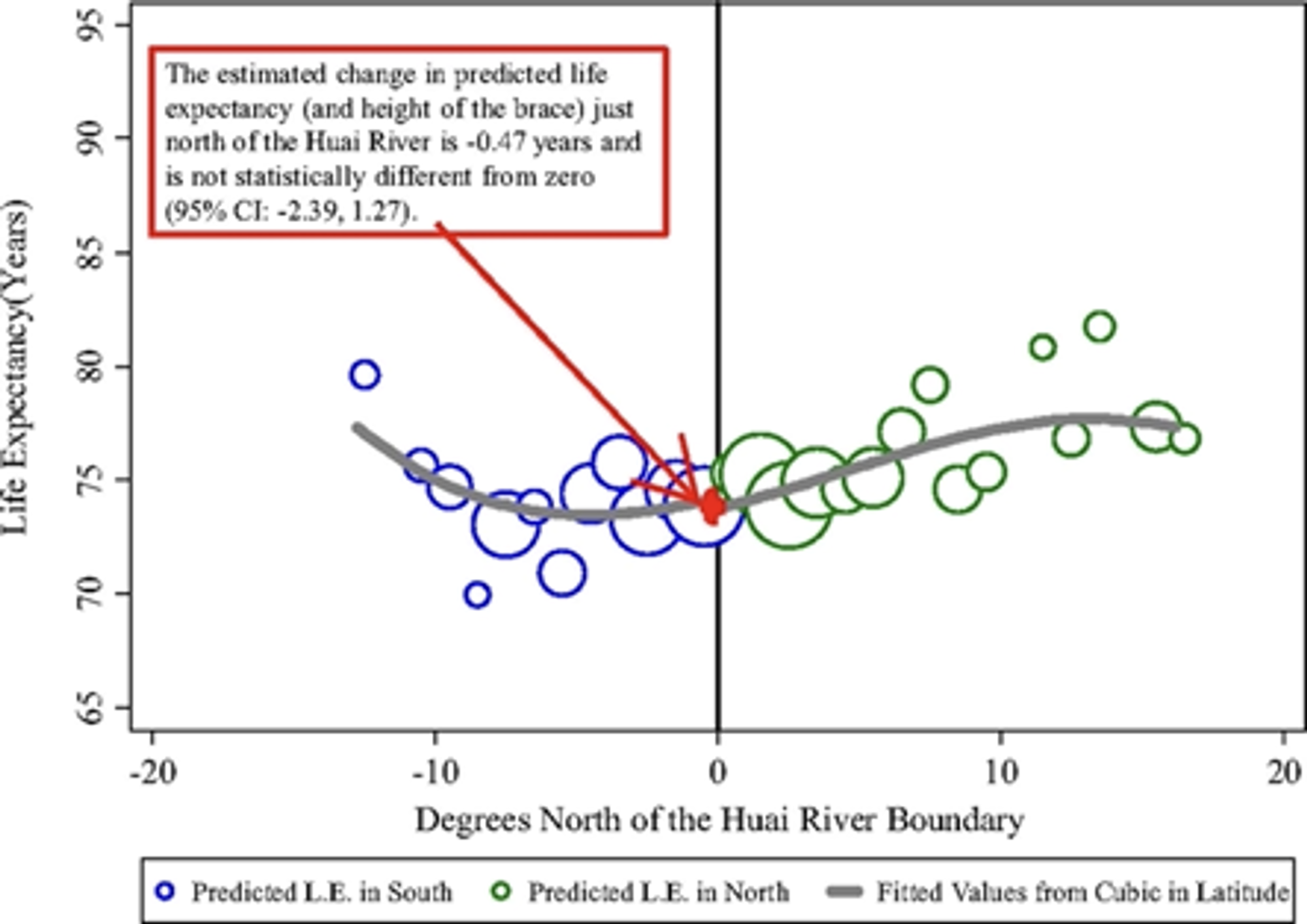
北側と南側のそれぞれで平均寿命を推定するモデルを学習して、その差分(下図中の赤線)が大気汚染対策の効果と見做せるとしています。問題は南北それぞれの平均寿命を推定するモデルにどのような変数を投入すべきかということですが、多項式項を含めて複雑な表現力を持つモデルの方(下図の上側)が効果が大きくなるので、論文中ではそちらのモデルを採用しています。この変数選択が恣意的であるということで、批判を受けることになりました。
変数選択が効果量の推定に大きく影響を与えるので、この問題においては変数選択は重要だということになります。
予測タスクと推論タスクの違い
変数選択が重要な場合とそうでない場合について、予測タスクと推論タスクの違いとして説明してみたいと思います。
例えば、「実車回数」を目的変数として、説明変数がたくさんある中で「利用頻度アンケート」が1単位増加した場合の「実車回数」への影響を知りたいとします。
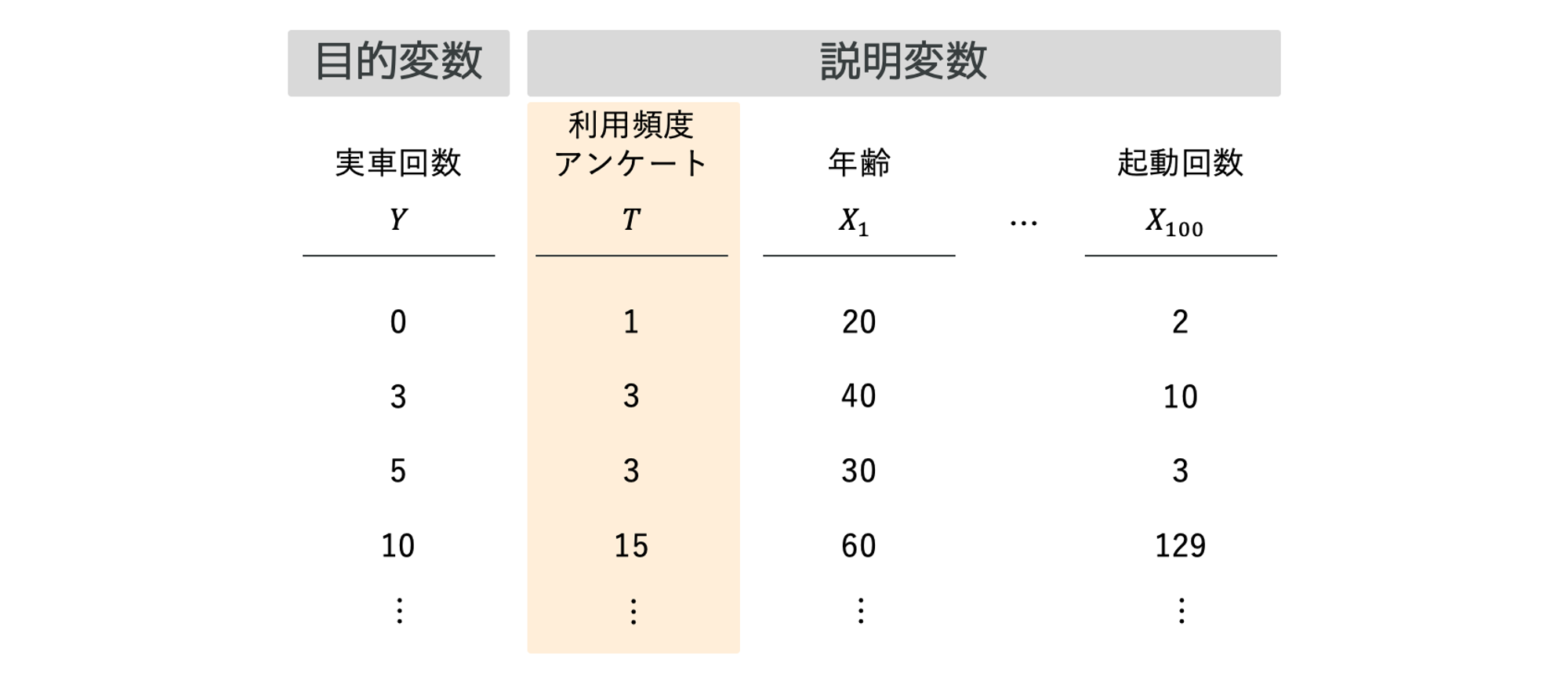
この問題に対して、機械学習モデルを何も考えずに適用すると、目的変数と予測値の差が小さくなるように学習するので、「利用頻度アンケート」の係数がどのような値になるかについては気にしていません。これは、タスクを「予測タスク」として処理しているからです。

予測タスク
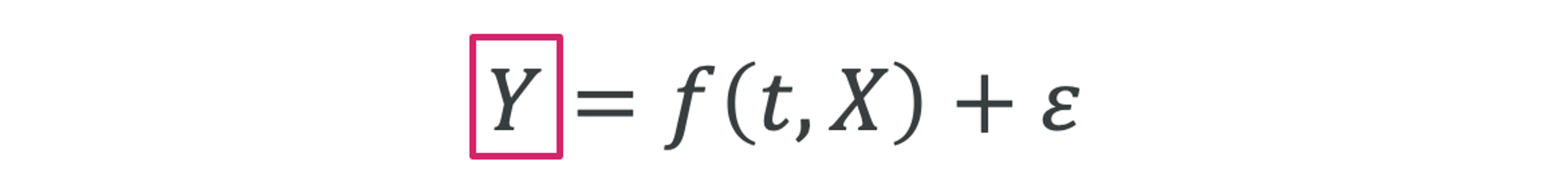
予測タスクはGround truthのに対して、より良い近似値であるが得られれば良く、モデル内部のパラメータ(を含む)に興味はありません。また、推定誤差であるは小さい方が良く、ground truthが分かっているからこそ、モデルの性能評価はしやすいです。
推論タスク
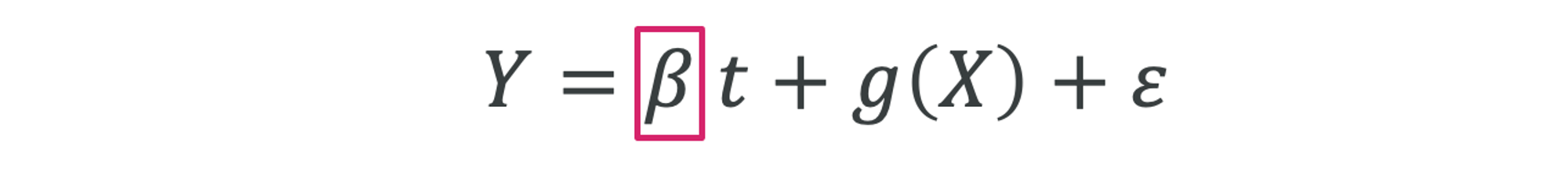
一方で、推論タスクは特定のパラメータの推定値以外には興味が無く、極論を言えばモデルの出力であるや誤差がどのような値であるかは興味がありません。パラメータの推定誤差を小さくしたいのですが、のground truthは不明で評価を難しくしています。
先ほどの大気汚染対策の効果を推定する問題は、まさに推論タスクであり、推論タスクにおいてはをなるべく正しく推定するために変数選択が重要だったというわけです。
変数選択のシミュレーション
実際にはの真値が分からないため、を推定するための変数選択が正しく行われているか評価できないのですが、今回はを推定するための手法を比較したいので、真のが分かっているシミュレーションで確認してみたいと思います。
データ生成過程
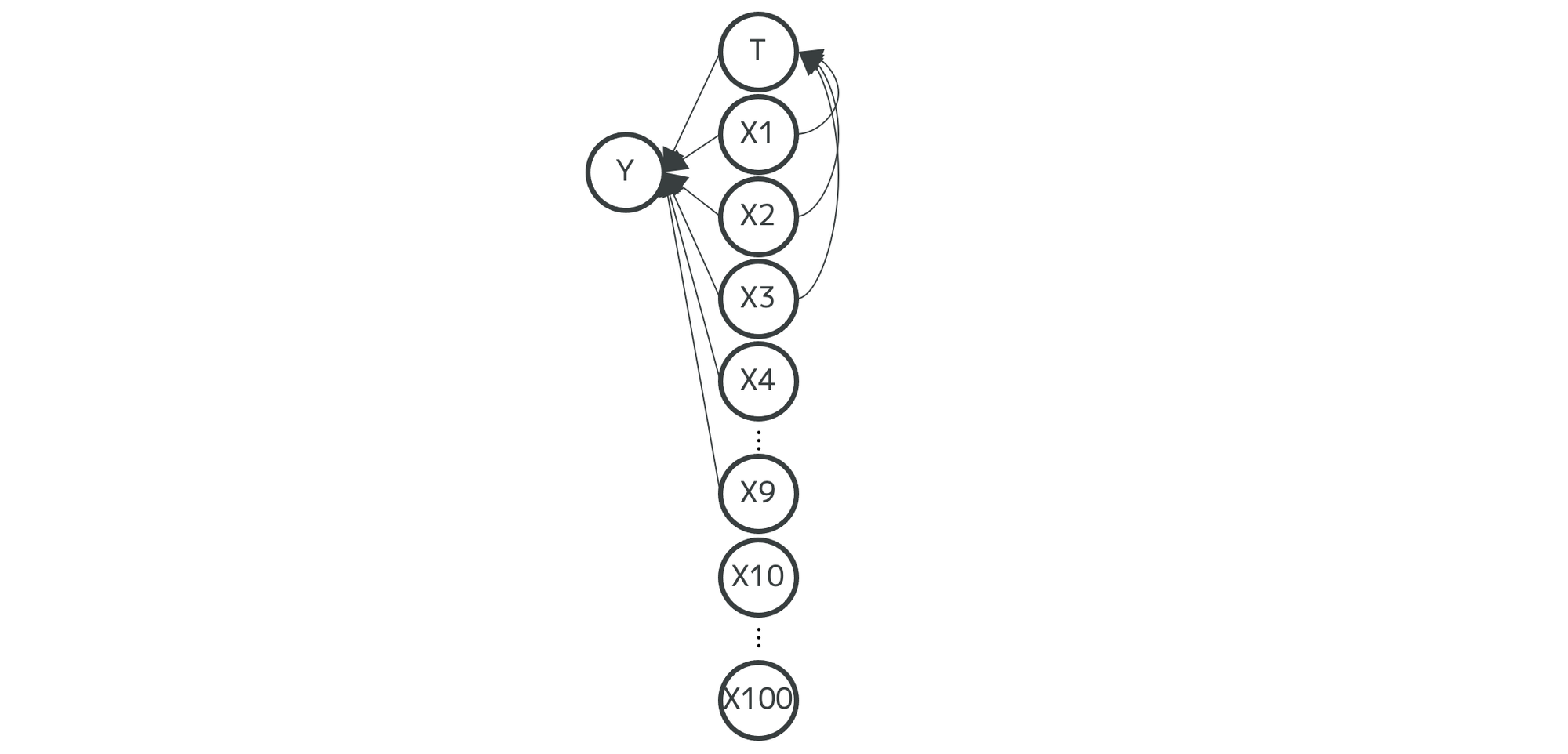
データ生成過程は以下のように設定します
- はとの10個の変数で決まる
- の係数が推定したいパラメータで、真値が1であると分かっているとする
- はの3個の変数で決まる
- はともとも無関係な変数であるとする
データ生成コード
import numpy as np
import pandas as pd
nObs = 100
nVar = 100
nSim = 100
np.random.seed(0)
df_sim = pd.DataFrame(
np.random.normal(loc=0, scale=1, size=(nObs * nSim, nVar)),
columns=["X" + str(i) for i in range(1, 101)])
# TはX1, X2, X3からpathがある
df_sim["T"] = df_sim["X1"] + df_sim["X2"] + df_sim["X3"] + 0.2 * np.random.normal(loc=0, scale=1, size=nObs * nSim)
# YはT, X1〜X9からpathがある(X10〜X100は無関係なデータ) # Tの係数βの真値は1である
df_sim["Y"] = (
1 * df_sim["T"]
+ 10 * df_sim["X1"] + 10 * df_sim["X2"] + 10 * df_sim["X3"]
+ 10 * df_sim["X4"] + 10 * df_sim["X5"] + 10 * df_sim["X6"]
+ 10 * df_sim["X7"] + 10 * df_sim["X8"] + 10 * df_sim["X9"]
+ np.random.normal(loc=0, scale=1, size=nObs * nSim) )
# シミュレーション実行回数に応じたSimNumberを付与する
df_sim["SimNumber"] = df_sim.index.values // nSim + 1そもそも変数選択して、うまくが推定できるのか?
はじめに、変数選択が理想的に行われたとして、の推定がうまくできるのかを確認してみましょう。データ生成過程が分かっているので、とそれ関係するを説明変数として、重回帰を学習させてみます。
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
import seaborn as sns
sim = list()
for name, group in df_sim.groupby("SimNumber"):
y = group["Y"]
x = group[["X1", "X2", "X3", "X4", "X5", "X6", "X7", "X8", "X9", "T"]]
model = LinearRegression().fit(x, y)
sim.append({"SimulationNumber": name, "estimate": model.coef_[x.columns.to_list().index('T')]})
df_results_true = pd.DataFrame(sim)
df_results_true["estimate"].plot(kind="kde", figsize=(10, 6))
plt.axvline(1, linestyle="--", color="red", label="ols effect")
plt.xlabel("Estimate")
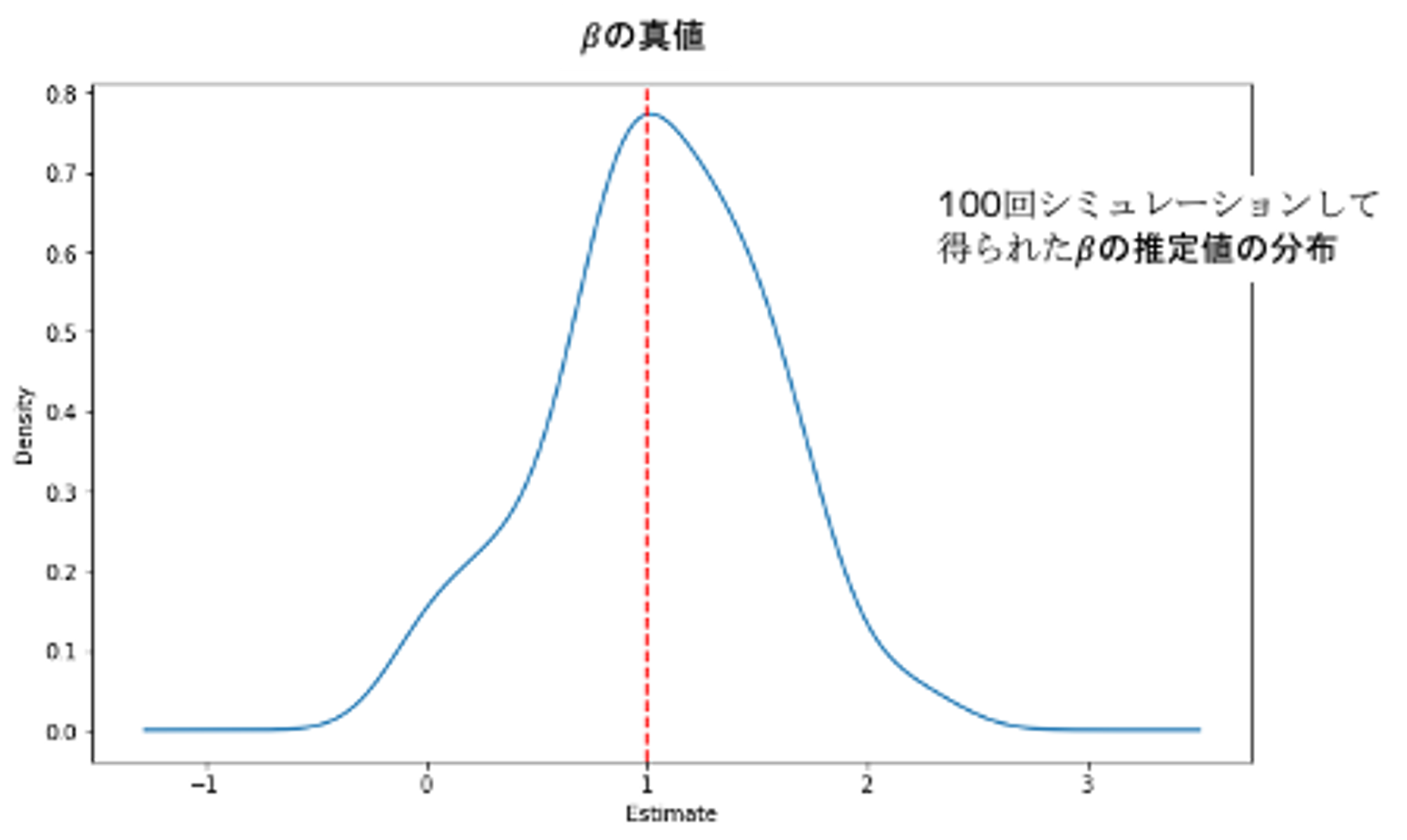
plt.show()推定されたは真値の1に近い値と推定されています。ただ、このモデルはデータ生成過程を知っている神様目線なので、実務上はほぼ不可能です。
変数選択しないとの推定はどうなる?
もう一つ確認しておきたいこととして、変数選択をせずにを推定した場合はどうなるのでしょうか?
sim = list()
for name, group in df_sim.groupby("SimNumber"):
y = group["Y"]
x = group.drop(columns=["Y", "SimNumber"])
model = LinearRegression().fit(x, y)
sim.append({"SimulationNumber": name, "estimate": model.coef_[-1]})
df_results_ols = pd.DataFrame(sim)
df_results_ols["estimate"].plot(kind="kde", figsize=(10, 6))
plt.axvline(1, linestyle="--", color="red", label="ols effect")
plt.xlabel("Estimate")
plt.show()推定されたは真値1より大きくズレた推定値となっています。無関係な変数が推定の邪魔をしているようです。
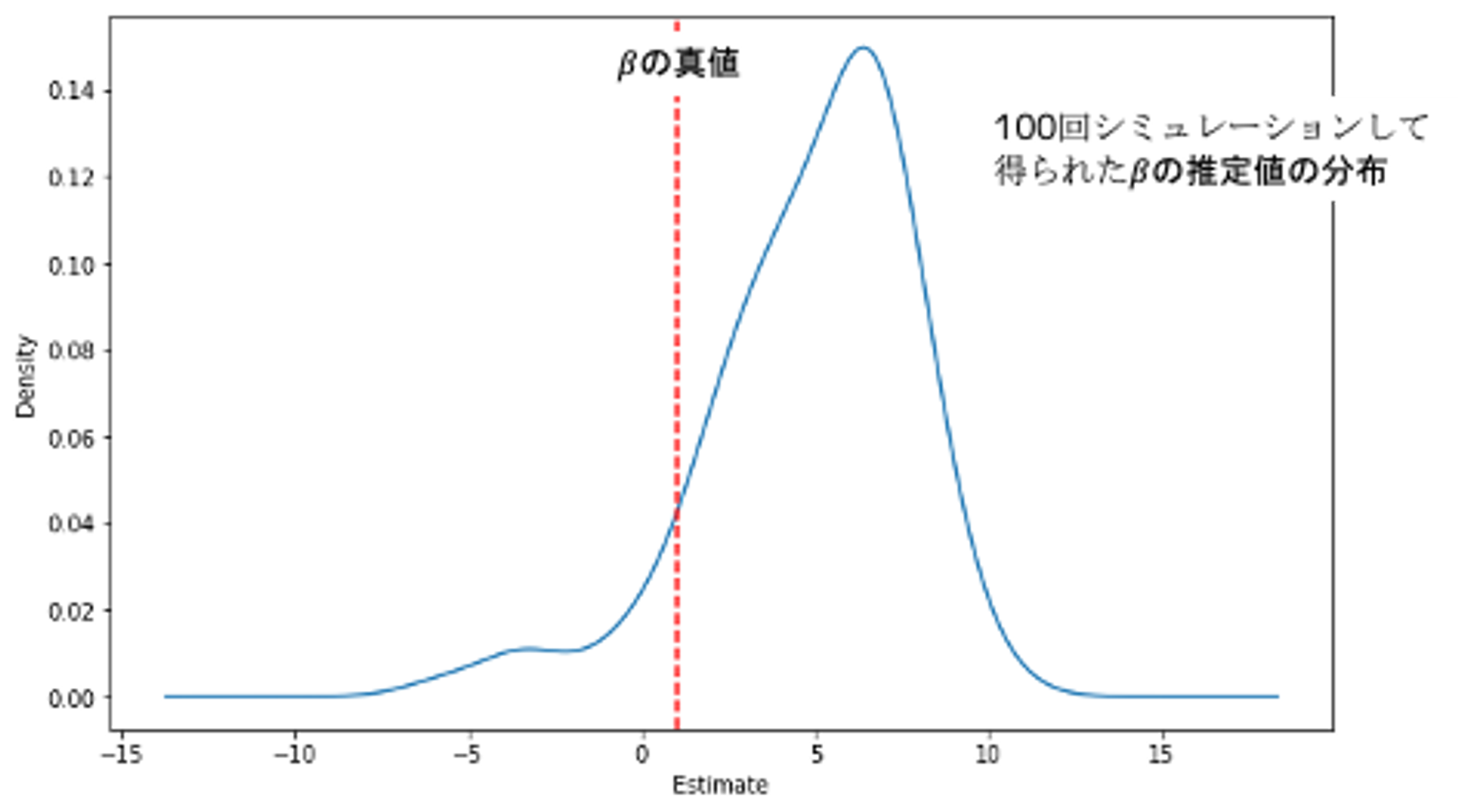
変数選択をそのまま適用するとの推定はどうなる?
では、変数選択を何も考えずに適用した場合、の推定値はどのようになるでしょうか?今回はLassoで変数選択を行ってから重回帰をしてみたいと思います。
from sklearn.linear_model import LassoCV
sim = list()
for name, group in df_sim.groupby("SimNumber"):
# LassoCVで変数選択を行う
y = group["Y"]
x = group.drop(columns=["Y", "SimNumber"])
model_lasso = LassoCV(cv=10, random_state=0).fit(x, y)
coef = pd.Series(model_lasso.coef_, index=x.columns)
# OLSでestimateを出す
selected_cols = coef[coef != 0.0].index.to_list()
if 'T' not in selected_cols:
selected_cols = selected_cols.append('T')
x_new = x[selected_cols]
model = LinearRegression().fit(x_new, y)
sim.append({"SimulationNumber": name, "estimate": model.coef_[selected_cols.index('T')]})
df_results_naive_lasso = pd.DataFrame(sim)
df_results_naive_lasso["estimate"].plot(kind="kde", figsize=(10, 6))
plt.axvline(1, linestyle="--", color="red", label="ols effect")
plt.xlabel("Estimate")
plt.show()の推定値は真値から遠くなってしまいました。単に変数選択してもの真値にはたどり着かないようです。
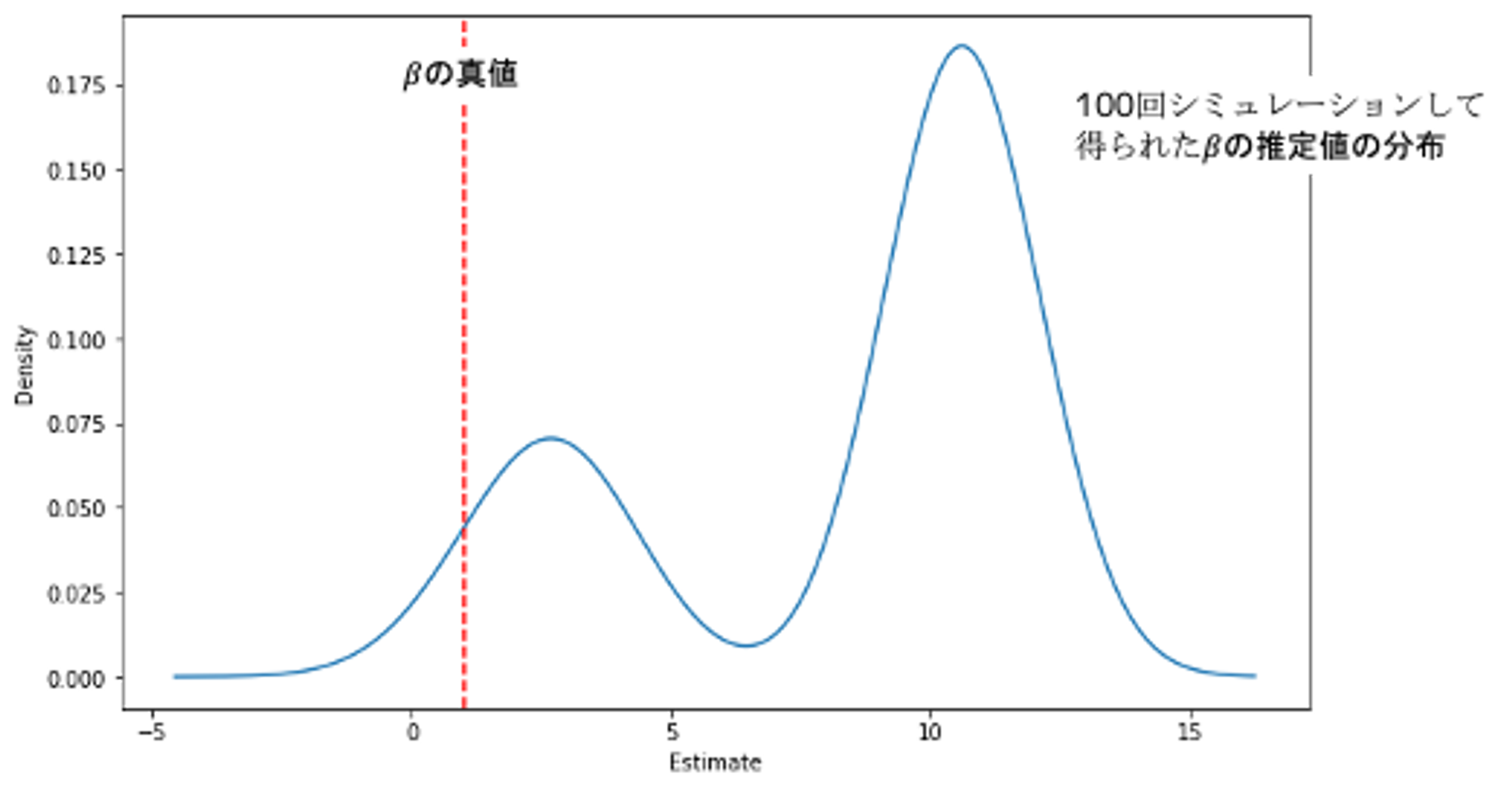
どのような方針で変数選択をしたら良いのか?
Double Selection
以下の回帰式におけるパラメータに興味があるとします
このとき、以下の3ステップでパラメータを推定します
- をで回帰して、残差を得る
- をで回帰して、残差を得る
- の残差をの残差で回帰する
Frisch-Waugh-Lovell theorem(FWL定理)によりとなります。
イメージとしてはの影響を除いたと、の影響を除いたの残差on残差で回帰することにより、の影響が除かれたが手に入るというものになります。
def get_residuals(dependent_var, df):
# LassoCVで変数選択を行う
model_lasso = LassoCV(cv=10, random_state=0).fit(df, dependent_var)
coef = pd.Series(model_lasso.coef_, index=df.columns)
# 選択された変数でOLSを行う
selected_cols = coef[coef != 0.0].index
df_new = df[selected_cols]
model = LinearRegression().fit(df_new, dependent_var)
# 残差を計算する
residuals = (dependent_var - model.predict(df_new))
return residuals
sim = list()
for name, group in df_sim.groupby("SimNumber"):
resid_y = get_residuals(group["Y"], group.drop(columns=["Y", "T", "SimNumber"]))
resid_t = get_residuals(group["T"], group.drop(columns=["Y", "T", "SimNumber"]))
y = pd.DataFrame({"resid_y": resid_y})
x = pd.DataFrame({"resid_t": resid_t})
model = LinearRegression().fit(x, y)
sim.append({"SimulationNumber": name, "estimate": model.coef_[0][0]})
df_results_cvDS = pd.DataFrame(sim)
df_results_cvDS["estimate"].plot(kind="kde", figsize=(10, 6))
plt.axvline(1, linestyle="--", color="red", label="ols effect")
plt.xlabel("Estimate")
plt.show()回帰を3ステップに分けて残差on残差の回帰を行っただけですが、真のに近くなりました。
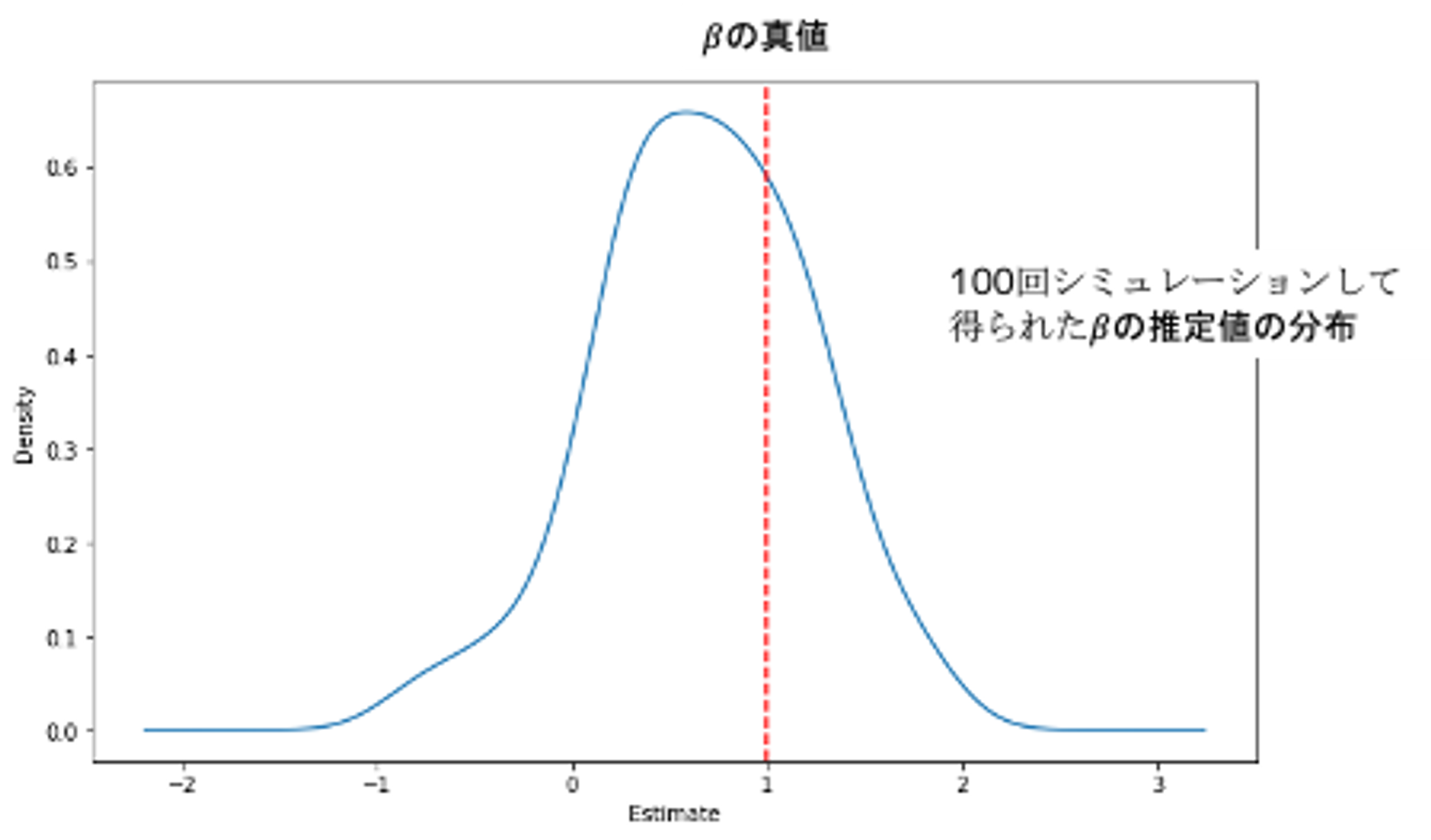
Regorous Lasso
Cross ValidationでLassoのを探索するとoverfitする可能性が残っています。
Rigorous Lassoでは理論的に最適なの推定値が手に入るので、これを使っての推定値を入手してみましょう。
from rpy2.robjects.packages import importr
from rpy2.robjects import numpy2ri
base = importr("base")
hdm = importr("hdm")
sim = list()
numpy2ri.activate()
for name, group in df_sim.groupby("SimNumber"):
x_r = group.drop(columns=["Y", "T", "SimNumber"]).values
y_r = group[["Y"]].values
t_r = group[["T"]].values
model_rlasso = hdm.rlassoEffect(x=x_r, y=y_r, d=t_r, method="partialling out")
summary = base.summary(model_rlasso)
sim.append({"SimulationNumber": name, "estimate": summary[0][0][0]})
df_results_rlassoDS = pd.DataFrame(sim)
numpy2ri.deactivate()
df_results_rlassoDS["estimate"].plot(kind="kde", figsize=(10, 6))
plt.axvline(1, linestyle="--", color="red", label="true effect")
plt.xlabel("Estimate")
plt.show()単純なDouble Selectionよりも真値に近いが入手できました。
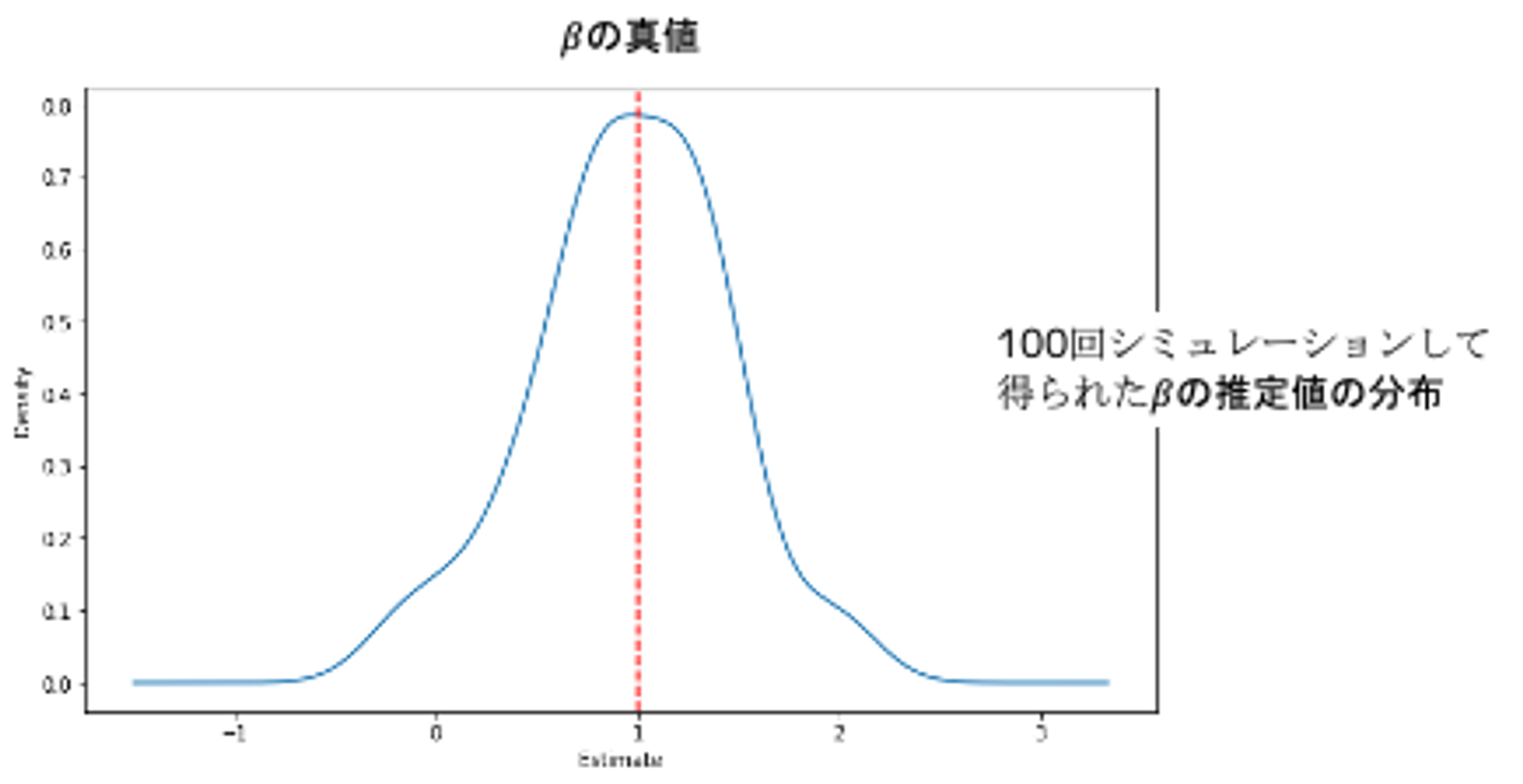
Double Machine Learning
Double Selectionでは、残差を求める箇所に線型モデルを使用していました。この部分に任意の機械学習モデルを使用するのがDouble Machine Learningです。
以下の回帰式におけるパラメータ𝛽に興味があるとします。
このとき、以下の3ステップでパラメータを推定します
- をで回帰して、残差を得る
- をで回帰して、残差を得る
- の残差をの残差で回帰する
Honest LearningとCross-fitting DML
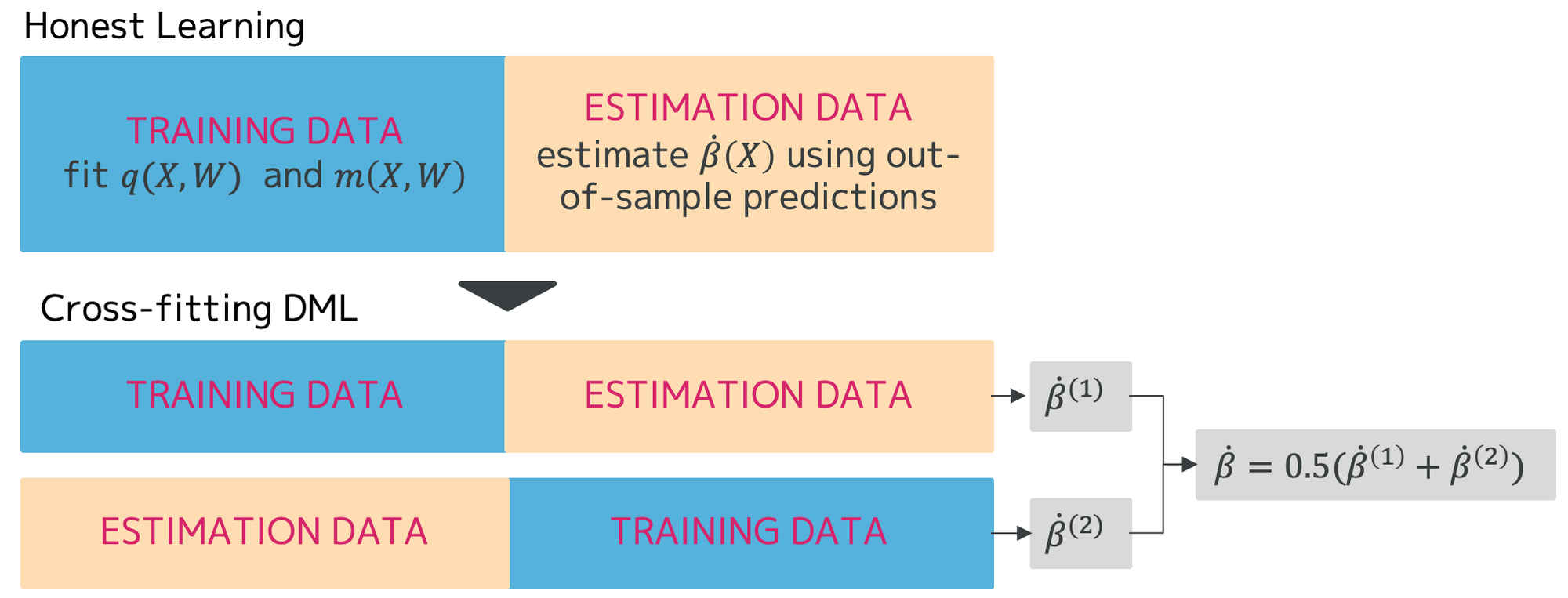
Double Machine Learningは各ステップで機械学習モデルを学習するため、Overfitによるバイアスが発生します。このバイアスを除去するために、データを2つに分割して、一方でとを求め、もう一方でを求めるHonest Learningという手法があります。このHonest Learningを発展させて、分割したデータをを入れ替えて学習し、それぞれで入手できたの平均をの推定値とするCross-fitting DMLという手法がありますので、今回はこれを使用してみます。
def dml_estimator(df_1, df_2):
model_cv_lasso_y = LassoCV(cv=10, random_state=123).fit(df_1.drop(columns=["Y", "T"]), df_1["Y"])
model_cv_lasso_t = LassoCV(cv=10, random_state=123).fit(df_1.drop(columns=["Y", "T"]), df_1["T"])
predict_y = model_cv_lasso_y.predict(df_2.drop(columns=["Y", "T"]))
predict_t = model_cv_lasso_t.predict(df_2.drop(columns=["Y", "T"]))
resid_y = df_2["Y"] - predict_y
resid_t = df_2["T"] - predict_t
return (resid_t * resid_y).mean() / (resid_t * resid_t).mean()
def dml_crossfit(df_1, df_2):
est1 = dml_estimator(df_1, df_2)
est2 = dml_estimator(df_2, df_1)
return 0.5 * est1 + 0.5 * est2
sim = list()
for name, group in df_sim.groupby("SimNumber"):
df_1 = group.drop(columns=["SimNumber"]).sample(frac=0.5, random_state=123)
df_2 = group.drop(columns=["SimNumber"]).drop(df_1.index)
est = dml_crossfit(df_1, df_2)
sim.append({"SimulationNumber": name, "estimate": est})
df_results_DML = pd.DataFrame(sim)
df_results_DML["estimate"].plot(kind="kde", figsize=(10, 6))
plt.axvline(1, linestyle="--", color="red", label="true effect")
plt.xlabel("Estimate")
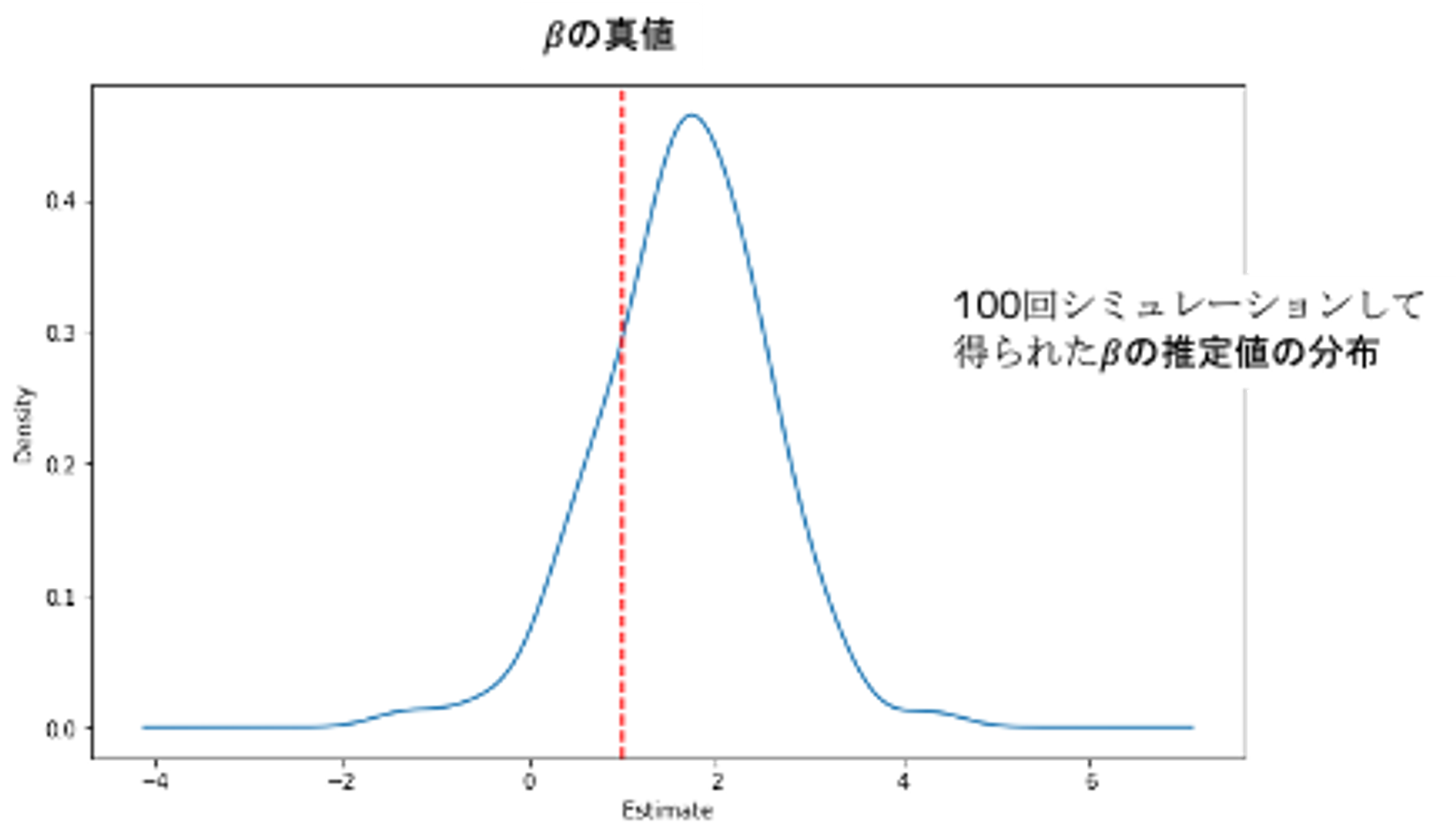
plt.show()の推定値は真値とはズレていますが、これはHonestにより学習データが減少していてUnderfitしている可能性があります。
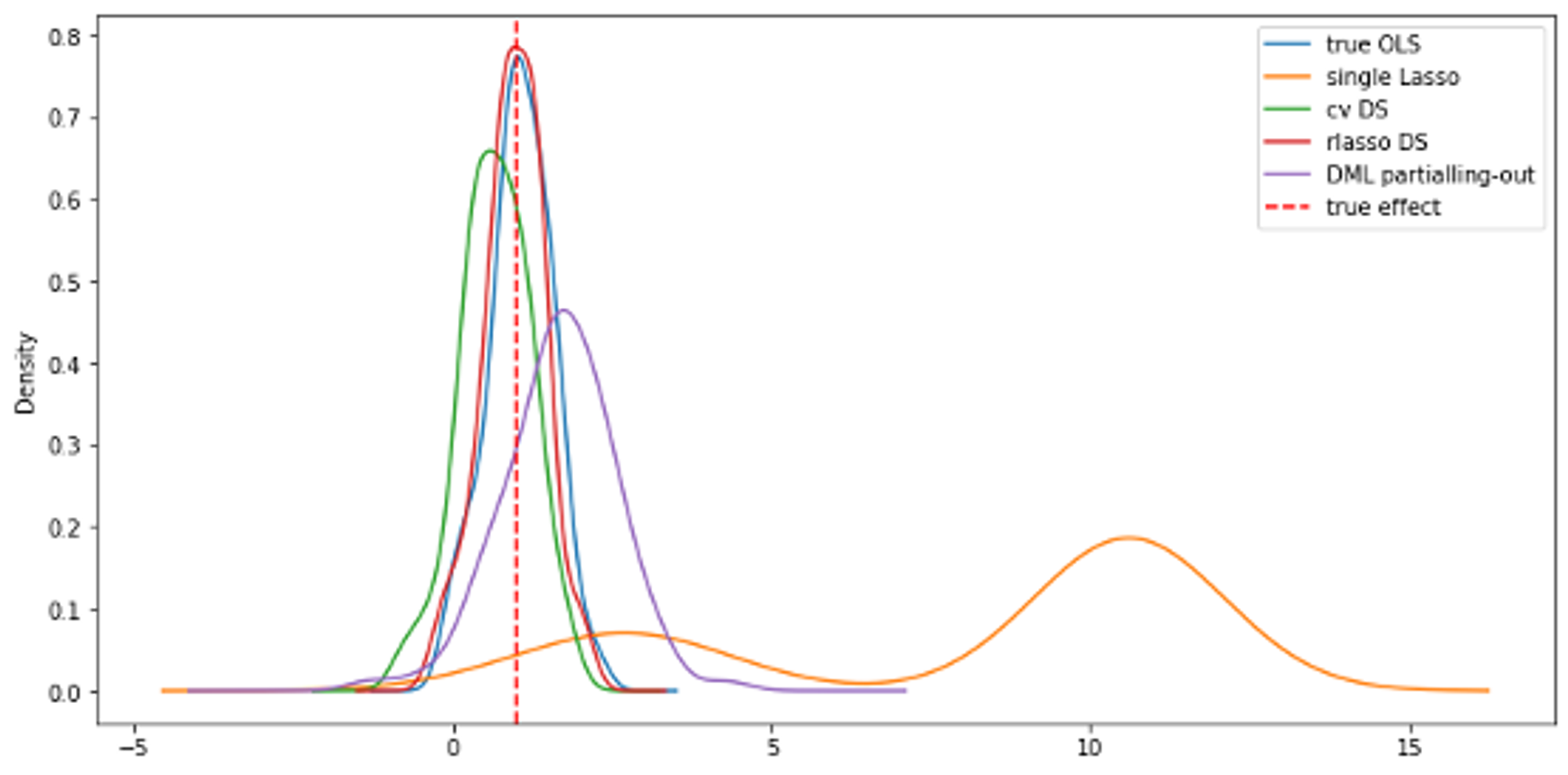
各手法の推定値比較
今回のシミュレーションにおけるの推定値を並べてみましょう。今回の問題に関しては、Regorous Lassoの推定が真値に近いという結果になりました。ただし、これは特定の手法が優れているということではなく、今回のデータの特性に合っていたとみるべきでしょう。改めてデータ生成コードを見ると、1回のシミュレーションでわずか100レコードしか生成していないので、データ量の少なさによる機械学習モデルのunderfitなどが影響していると考えられます。
さいごに
今回は、特定の変数におけるパラメータを求めるにあたって、変数選択の重要性とDouble Selection、Double Machine Learningの手法を紹介しました。
興味のあるパラメータを求めるのに、機械学習の単純適用で良いのかという点は、ビジネスでも頻繁に考えさせられるところです。
We're Hiring!
Twitter @mot_techtalk のフォローもよろしくお願いします!

